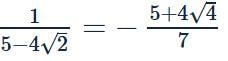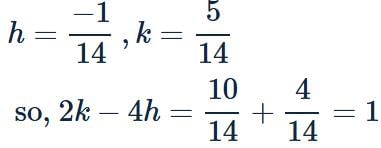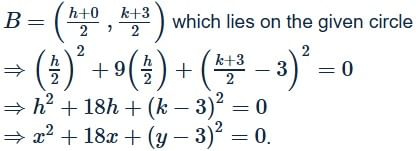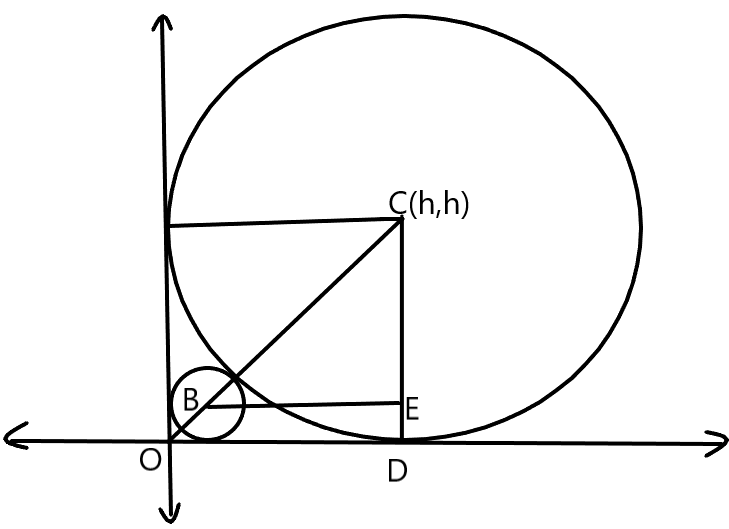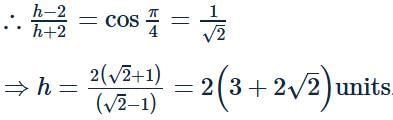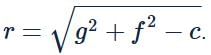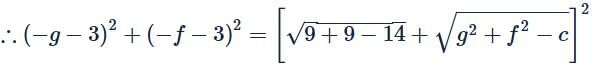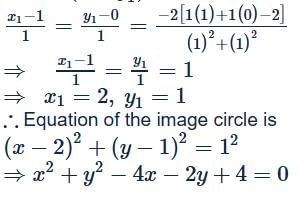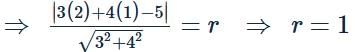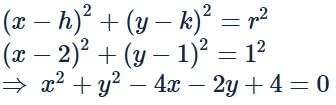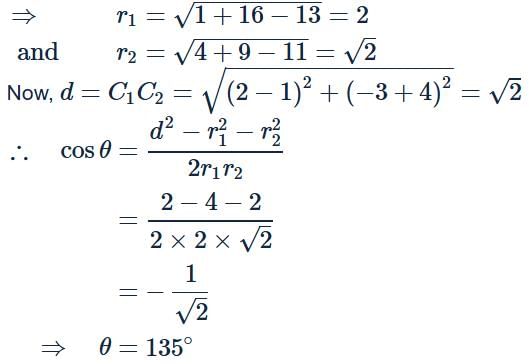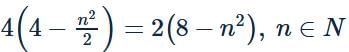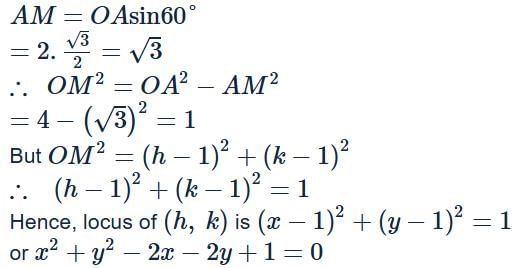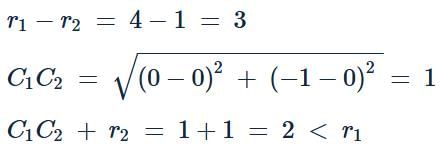Test: Conic Sections - 1 - JEE MCQ
25 Questions MCQ Test - Test: Conic Sections - 1
If the line 2x – y + λ = 0 is a diameter of the circle x2+y2+6x−6y+5 = 0 then λ =
Length of common chord of the circles x2+y2+2x+6y = 0 and x2+y2−4x−2y−6 = 0 is
Let P(x1, y1) and P(x2, y2) are two points such that their abscissas x1 and x2 are the roots of the equation x2 + 2x − 3 = 0 while the ordinates y1 and y2 are the roots of the equation y2 + 4y − 12 = 0.Then the centre of the circle with PQ as diameter is
From a point P(3,3) on the circle x2+y2=18 two chords PQ and PR each of length 2 units are drawn on this circle. Then, the value of the length PM is equal to (where, M is the midpoint of the line segment joining Q and R)
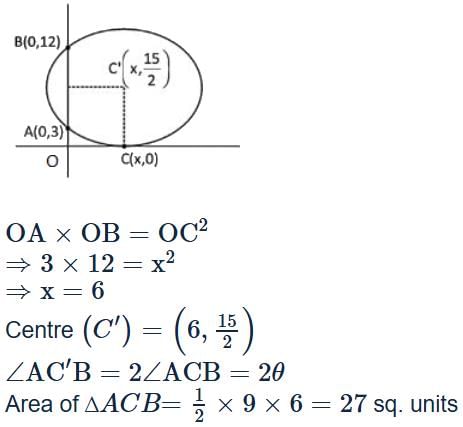
For a ∆ABC the vertices are A(0,3), B(0,12) and C(x,0). If the circumcircle of ΔABC touches the x-axis, then the area (in sq. units) of the ∆ABC is
Two perpendicular tangents to the circle x2+y2 = r2 meet at P. The locus of P is
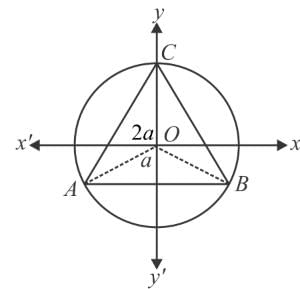
The equation of a circle with origin as a centre and passing through vertices of an equilateral triangle whose median is of length 3a, is
The equation of the circle whose diameter is the common chord of the circles x2 + y2 + 2x + 3y + 2 = 0 and x2 + y2 + 2x − 3y − 4 = 0 is
A, B, C are points on the circle x2 + (y − 2)2 = a2 and α,β,γ are the parameters of the points A,B,C, if the ΔABC is equilateral, then:
If there is a point (x,y) on circle x2+y2−4x−6y−3=0, then maximum value of 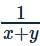 is
is
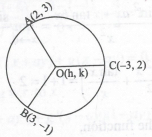
Let A(2,3),B(3,−1) and C(−3,2) be three points. If the centre of the circle passing through A,B and C is (h,k), then 2k−4h=
The length of tangent from the point (2, - 3) to the circle 2x2+2y2 = 1 is
The number of points with integral coordinates which are interior to the circle (x − 2009)2 + (y − 2009)2 = 16, is
From the point A(0,3) on the circle x2+9x+(y−3)2=0, a chord AB is drawn and extended to a point M such that AM=2AB ( B lies between A & M). The locus of the point M is
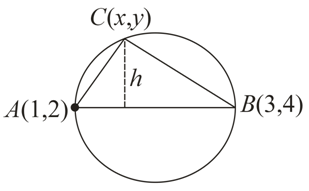
Let A(1, 2), B(3, 4) be two points and C(x, y) be a point such that area of ∆ABC is 3 sq. units and (x − 1)(x − 3) + (y − 2)(y − 4) = 0. Then number of positions of C, in the xy plane, is
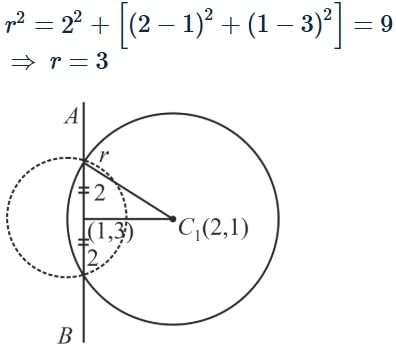
If one of the diameters of the circle x2 + y2 − 2x − 6y + 6 = 0 is a chord to the circle with centre (2, 1), then the radius of the circle is
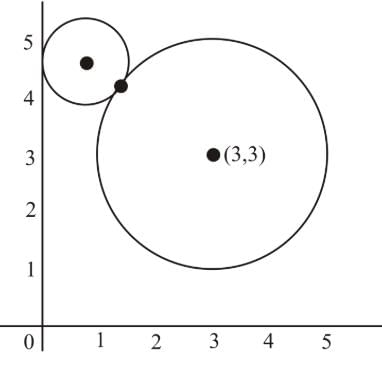
The radius of a bigger circle touching the circle x2 + y2 − 4x − 4y + 4 = 0 and both the coordinate axes, is
The locus of the centre of a circle, which touches externally the circle x2 + y2 − 6x − 6y + 14 = 0 and also touches Y-axis, is given by the equation
Equation of the circle which of the mirror image of the circle x2+y2−2x=0 in the line x+y=2 is:
The equation of the circle with centre (2, 1) and touching the line 3x+4y=5 is
The point (3,−4) lies on both the circles x2 + y2 − 2x + 8y + 13 = 0 and x2 + y2 − 4x + 6y + 11 = 0. Then, the angle between the circles is
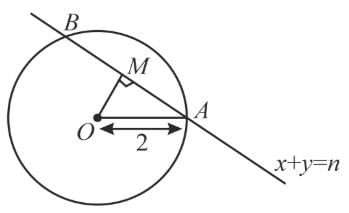
Find the sum of square of the length of the chords intercepted by the line x + y =n; n ∈ N on the circle x2 + y2 = 4.
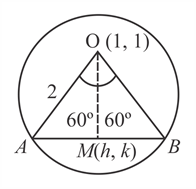
The locus of the midpoint of the chord of the circle x2 + y2 − 2x − 2y − 2 = 0 which makes an angle of 120° at the centre, is:
For the two circles, x2 + y2 = 16 and x2 + y2 − 2y = 0 there is/are



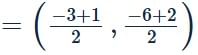
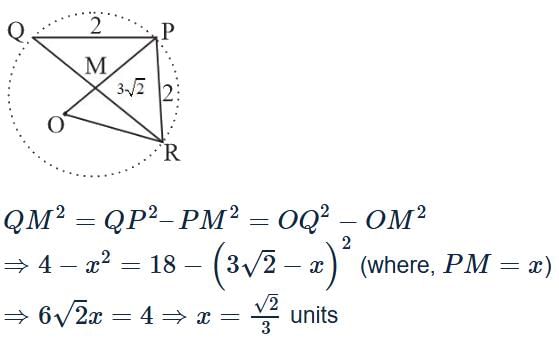

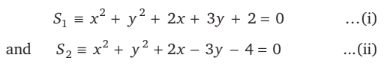
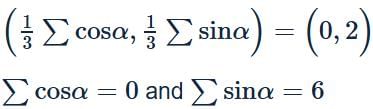
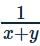 , value of (x+y) will be minimum, so (x + y) min = 5 + 4(−√2) = 5−4√2
, value of (x+y) will be minimum, so (x + y) min = 5 + 4(−√2) = 5−4√2