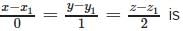Test: Introduction To Three Dimensional Geometry- 1 - JEE MCQ
25 Questions MCQ Test - Test: Introduction To Three Dimensional Geometry- 1
The distance of the point (3, 4, 5) from X- axis is
The direction cosines of X -axis are
The medians of a triangle are concurrent at the point called
The direction cosines of any normal to the XY plane are
How many lines through the origin make equal angles with the coordinate axes?
If the direction cosines of a straight line are < k , k , k > , then
Volume of a tetrahedron is k X area of one face X length of perpendicular from the opposite vertex upon it, where k is
The radius of the sphere through the points (4 ,3 , 0) , (0 , 4 , 3) ,(0 , 5 , 0) and (4 , 0 , 3) is
The points (4,7,8) ,(2, 3,4),(- 1, -2 , 1) and (1, 2, 5) are the vertices of a
The equation xy = 0 in three dimensional space represents
The graph of the equation x2+y2 = 0 in the three dimensional space is
In three dimensional space, locus of the equation x2+z2 = 0x2+z2 = 0 is
The distance of the point (x , y , z) from the XY –plane is
The angle between the lines x = 1 , y = 2 and y = - 1 , z = 0 is
The equation (x – 1) (x – 2) = 0 represents, in three dimensional space, a
A point (x , y , z) moves parallel to X- axis. Which of the three variables x , y , z remain fixed ?
A point (x , y , z) moves parallel to XY - plane. Which of the three variables x, y, z remain fixed ?
The plane x=0 divides the joinning of (−2,3,4) and (1,−2,3) in the ratio :
The direction cosines of the line joining (1 , - 1 , 1) , and (-1 , 1 , 1) are
The locus of the equation xy + yz = 0 is
The number of spheres of a given radius r and touching the coordinate axes is