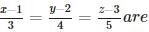Test: Introduction To Three Dimensional Geometry- 2 - JEE MCQ
25 Questions MCQ Test - Test: Introduction To Three Dimensional Geometry- 2
The distance between the planes 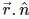 = p1 and
= p1 and 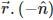 = p2 is
= p2 is
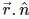 = p1 and
= p1 and 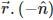 = p2 is
= p2 isThe point equidistant from the points (0 , 0 , 0) , (1 , 0 , 0) , (0 , 2 , 0) , and (0 , 0 , 3) is
The points (1 , 1 , 0) , (0 , 1 , 1) , (1 , 0 , 1) , and (2/3 , 2/3 , 2/3) are
The lines l1 and l2 intersect. The shortest distance between them is
Volume of a tetrahedron is k X area of one face X length of perpendicular from the opposite vertex upon it, where k is
A, B, C and D are four points in spaces such that AB = BC = CD = DA. Then ABCD is a
The foot of perpendicular from (α,β,γ) on Y axis is
The centre of the sphere , which passes through (a , 0 , 0) , (0 , b , 0) (0 , 0 , c) and (0 , 0 ,0) is abc ≠ 0
A sphere through three non – collinear points A, B, and C is smallest when its centre is
Three planes x + y = 0, y + z = 0, and x + z = 0
The centre of the sphere through the points (0 , 3 , 4) , (0 , 5 , 0) , (4 , 0 , 3) and (- 3 , 4 , 0) is
The points A (0 , 0 , 0) , B (1 , √3 , 0) , C (2 , 0 , 0) and D (1 , 0 , √3) are the vertices of
The points A (0 , 2 , 0) , B (√3 , 1 , 0) , are the vertices of
The locus of a first degree equation in x, y, z is a
Area of ΔABC whose vertices A (- 1 , 2 , 3) , B (1, 1, 1) , and C (2 , - 1 , 3) is
The value of x for which the points (x , x , x) , (0 , - 1 , - 2) , (- 3 , - 4 , - 5) and (- 6 , - 7 , - 8) are non-coplanar is
G is the centroid of triangle ABC. If P.V. of the points G , A , B , C are respectively, 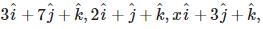 and
and 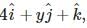 then (x, y) =
then (x, y) =
If the four points (3 , - 2 , - 1) , (2 , 3 , - 4) , (- 1 , 1 , 2) and (4 , 5, λ) are coplanar then λ is equal to
The number of spheres of a given radius which touch the coordinate planes is
The plane XOZ divides the join of (1 , -1 , 5) and (2 , 3 ,4) in the ratio k : 1, then the value of k is
In a three dimensional space, the equation 3x – 4y = 0 represents
The coordinates of the foot of perpendicular from the point A (1, 1 , 1) , on the line joining the points B (1 , 4 , 6) and C (5 , 4 , 4) are
The points (1, 2 , 3) , (- 1, -1 , - 1) and (3, 5 , 7) are the vertices of



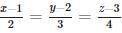 and
and