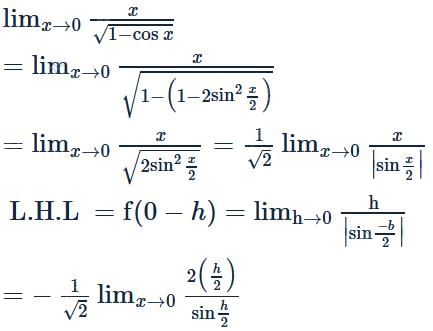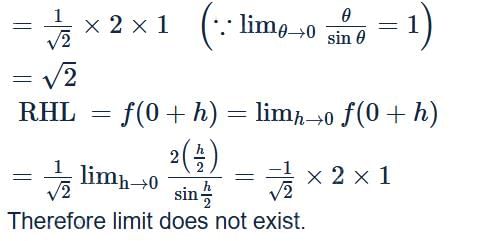Test: Limits And Derivatives - 1 - JEE MCQ
25 Questions MCQ Test - Test: Limits And Derivatives - 1
Let f (x) = x sin 1/x, x ≠ 0, then the value of the function at x = 0, so that f is continuous at x = 0, is
The positive integer n so that limx→3 (xn – 3n)/(x – 3) = 108 is
Let for a differentiable function f: (0, ∞) → R, f(x) - f(y) ≥ logₑ(x/y) + x - y, ∀ x, y ∈ (0, ∞). Then ∑ from n = 1 to 20 of f'(1/n²) is equal to __.
Let f(x) = x³ + x² f'(1) + x f''(2) + f'''(3), x ∈ ℝ. Then, f'(10) is equal to:
Suppose f(x) = 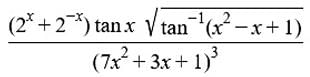 then the value of f(0) is equal to
then the value of f(0) is equal to
Let y = logₑ( (1 - x²) / (1 + x²) ), -1 < x < 1. Then at x = 1/2, the value of 225(y' - y'') is equal to:
lim (n → ∞) { (21/2 - 21/3) (21/2 - 21/5) ... (21/2 - 21/(2n+1))} is equal to
If α > β > 0 are the roots of the equation ax² + bx + 1 = 0, and
lim (x → 1/α) { (1 - cos(x² + bx + a)) / (2(1 - ax)²) }^(1/2) = 1/k ( (1/β) - (1/α) ), then k is equal to ____
If 2xy + 3yx = 20, then dy / dx at (2, 2) is equal to:


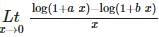 is equal to
is equal to 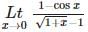 is equal to
is equal to
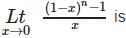
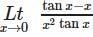 is equal to
is equal to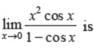
 is equal to
is equal to 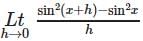 is equal to
is equal to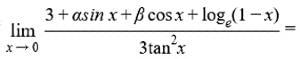 1/3, then 2α - β is equal to:
1/3, then 2α - β is equal to: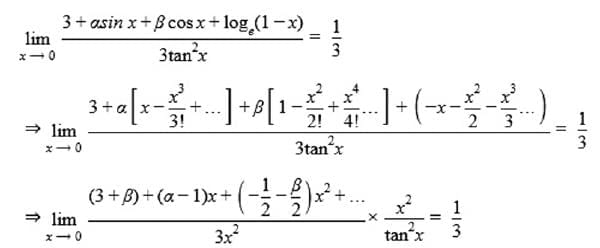

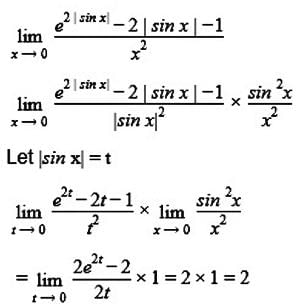
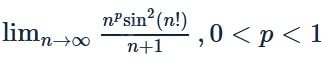 is equal to
is equal to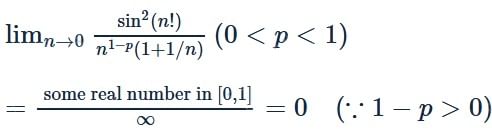
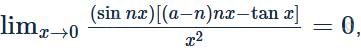 then the value of a is:
then the value of a is: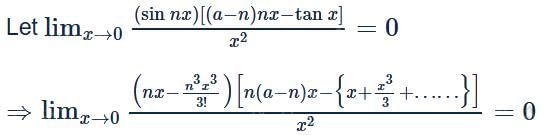
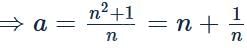

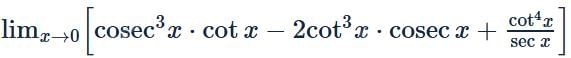 is equal to
is equal to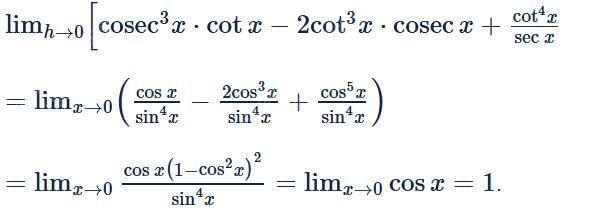
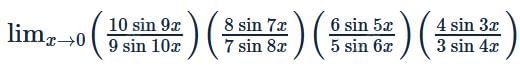
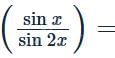
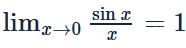
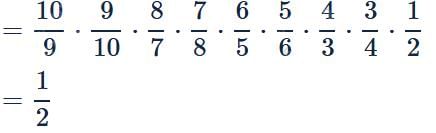
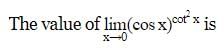
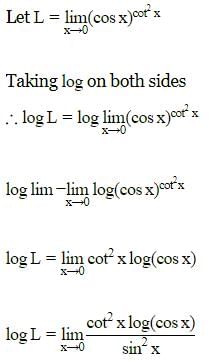

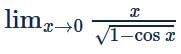 equal to?
equal to?