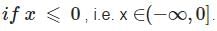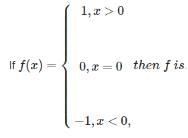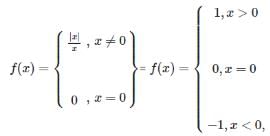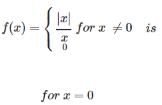Test: Relations & Functions- 2 - JEE MCQ
25 Questions MCQ Test - Test: Relations & Functions- 2
R = {(1, 1), (2, 2), (1, 2), (2, 1), (2, 3)} be a relation on A = {1, 2, 3}, then R is
If R is a relation from a set A to a set B and S is a relation from B to C, then the relation S ∘ R.
Let A be the set of all students of a boys school. The relation R in A given by R = {(a, b) : a is sister of b} is
Let A = {1, 2, 3}. Which of the following is not an equivalence relation on A ?
The binary operation * defined on the set of integers as a∗b = |a−b|-1 is:
Let T be the set of all triangles in a plane with R a relation in T given by R = {(T1, T2) : T1 is congruent to T2}. Then R is
If A is a finite set containing n distinct elements, then the number of relations on A is equal to
R is a relation from { 11, 12, 13} to {8, 10, 12} defined by y = x – 3. The relation R−1
If A = {(1, 2, 3}, then the relation R = {(2, 3)} in A is
The period of the function f(x) = sin2x + tan x is
Let A = {1, 2, 3}, then the domain of the relation R = {(1, 1), (2, 3), (2, 1)} defined on A is
Given the relation R = {(1, 2), (2, 3)} on eht set {1, 2, 3}, the minimum number of ordered pairs which when added to R make it an equivalence
Let R = {(1, 3), (4, 2), (2, 4), (2, 3), (3, 1)} be a relations on the set A = {1, 2, 3, 4}. the relation R is
The relation R in the set Z of integers given by R = {(a, b): 2 divides a – b}(a, b) where a, b ∈ Z is
Let A contain n distinct numbers. How many bijections from A to A can be defined?
Number of relations that can be defined on the set A = {a, b, c, d} is
A relation R in a set A is called universal relation, if
Let R be the relation defined in the set A = {1, 2, 3, 4, 5, 6, 7} by R = {(a, b) : both a and b are either odd or even}. Then R is
If f(x) = x – x2, then f(a + 1) – f(a – 1) , a ∈ R is :