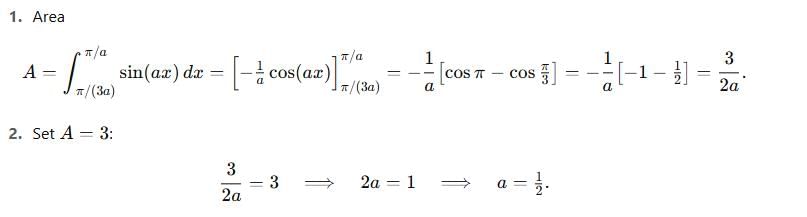Test: Application of Integrals- 6 - Commerce MCQ
25 Questions MCQ Test - Test: Application of Integrals- 6
The area lying in the first quadrant and bounded by the curve y = x3 , the x – axis and the ordinates at x = - 2 and x = 1 is
Area bounded by the curves satisfying the conditions 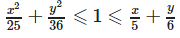 is given by
is given by
The area of the figure bounded by y = ex, y = e−x and the straight line x = 1 is
The area bounded by the parabolas y = (x+1)2 and y = (x−1)2 and the line y = (1/4) is equal to
The area enclosed between the curve y = loge(x+e) and x = loge 1/y and the x- axes is
The area bounded by the curve y = x3, the x – axis and two ordinates x = 1 and x = 2 is
The area bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is given by
The area enclosed between the curves y = √x , x = 2y+3and the x-axis is
The area of the region {(x , y) : x2+y2⩽1⩽x+y} is equal to
The area bounded by y = |sinx| , the x – axis and the line |x| = π is
If A is the area between the curve y = sin2x , x – axis and the lines x =
The area bounded by the curves y2 = x and y = x2 is
The positive value of the parameter a for which the area of the figure bounded by y = sin ax, y = π/a, and y = π/3a is 3 is equal to
The area bounded by the parabolas y = 5x2and y − 9 = 2x2 is
The area bounded by the curves y = √x , 2y+3 = x and the x – axis in the first quadrant is
The area bounded by y = 2cosx , x = 0 to x = 2π and the axis of x in square units is
The area common to the circle x2+y2 = 16a2 and the parabola y2 = 6ax is
The area bounded by the parabola y2 = 4x and the line x + y = 3 is
The area enclosed by the parabola y2 = 2x and its tangents through the point (-2 , 0) is
The area bounded by the curve y = x log x and y = 2x−2x2 is
The area of the figure bounded by the curve y = logex , the x – axis and the straight line x = e is
The area of the region bounded by the curves y = |x−1| and y = 3 - |x| is
The area bounded by the curve y = x2+1and the line x + y = 3 is
The area bounded by the angle bisectors of the lines x2−y2+2y = 1 and x+y = 3 is
The area bounded by the curves y= |x−1| and y = 1 is given by