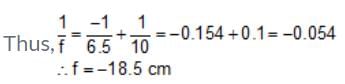Test: Lense Formula - Class 10 MCQ
10 Questions MCQ Test - Test: Lense Formula
An object is 9 cm from a magnifying lens and its image is formed 36 cm from the lens. Magnification of the lens is
An object 4 cm tall is placed in front of a convex lens. It produces an image 3 cm tall. What is the magnification of the lens ?
A convergent beam of light passes through a diverging lens of focal length 0.2 m and comes to focus 0.3 m behind the lens. Find the position of the point at which the beam would converge in the absence of lens.
An object is placed 10 cm from a diverging lens which forms an image 6.5 cm from the lens. What is the focal length of the lens ?
A convex lens of focal length 12 cm produces a magnification of -1. The object should be placed at;
An object is situated at a distance of f/2 from a convex lens of focal length f. Distance of image will be
A convex lens forms a real, inverted and same sized image as the object placed at a distance of 40 cm from it. The power of the lens is _____D.
A concave lens of 20 cm focal length forms an image 15 cm from the lens. What is the object distance ?
Where should an object be placed in front of convex lens so as to obtain the image formed on slide projector ?
The distance at which an object should be placed from a thin convex lens of focal length 10 cm to obtain a virtual image of double of its size is