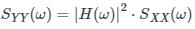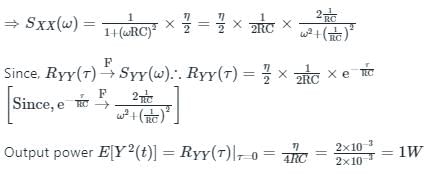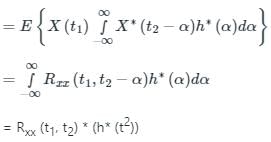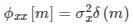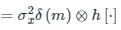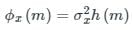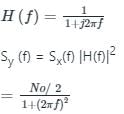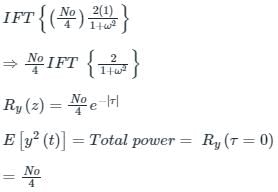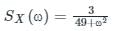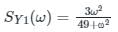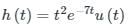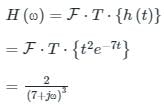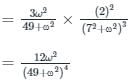Test: Transmission of Random processes through Linear Systems - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Transmission of Random processes through Linear Systems
Consider an LTI system subjected to a wide-sense stationary input {x(n)}, which is a white noise sequence. The cross-correlation ϕx[m] between the input x(n), and output y(n) is:
Where 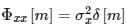 and h[⋅] is the impulse response.
and h[⋅] is the impulse response.
Where
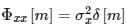 and h[⋅] is the impulse response.
and h[⋅] is the impulse response.A WSS random process having mean m is applied as input to LTI system having impulse response  . The mean of the output is same as the mean of the input. The value of a is _____
. The mean of the output is same as the mean of the input. The value of a is _____
 . The mean of the output is same as the mean of the input. The value of a is _____
. The mean of the output is same as the mean of the input. The value of a is _____Let X(t) be a wide sense stationary random process with the power spectral density SX(f) as shown in Figure (a), where f is in Hertz (Hz). The random process X(t) is input to an ideal lowpass filter with the frequency response:

This is as shown in Figure (b). The output of the lowpass filter is Y(t).
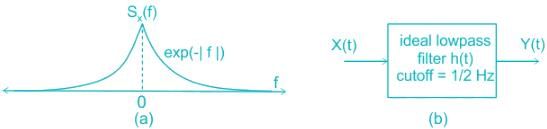
Let E be the expectation operator. Consider the following statements:
I. E(X(t)) = E(Y(t))
II. E(X2(t)) = E(Y2(t))
III. E(Y2(t)) = 2
Select the correct option:

This is as shown in Figure (b). The output of the lowpass filter is Y(t).
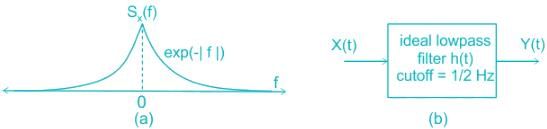
Let E be the expectation operator. Consider the following statements:
I. E(X(t)) = E(Y(t))
II. E(X2(t)) = E(Y2(t))
III. E(Y2(t)) = 2
Select the correct option:
Let X(t) be a wide sense stationary random process with the power spectral density SX(f) as shown in Figure (a), where f is in Hertz (Hz). The random process X(t) is input to an ideal lowpass filter with the frequency response:
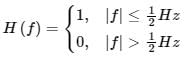
This is as shown in Figure (b). The output of the lowpass filter is Y(t).
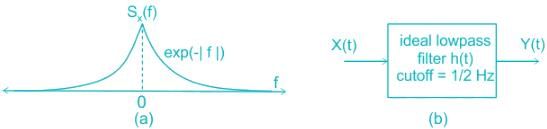
Let E be the expectation operator. Which of the following statements is/are correct?
Consider a white Gaussian noise process N(t) with two-sided power spectral density SN(f) = 0.5 W/Hz as input to a filter with impulse response 0.5e-t2/2 (t is in seconds) resulting in output Y(t). The power in Y(t), in watts, will be:
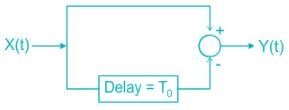
A wide sense stationary random process X(t) passes through the LTI system shown in the figure. If the autocorrelation function of X(t) is RX(τ), then the autocorrelation function RY(τ) of the output Y(t) is equal to
The two sided PSD of noise signal (PSD for the positive frequencies is shown in below figure) x(t) shown in figure is applied to RC LPF whose time constant is 1 ms.
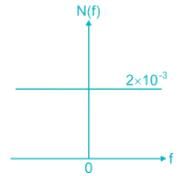
The output power P out is.
Consider an LTI system subjected to a wide-sense stationary input {x(n)}, which is a white noise sequence. The cross-correlation ϕx[m] between the input x(n), and output y(n) is:
Where 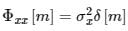 and h[⋅] is the impulse response.
and h[⋅] is the impulse response.
Let X(t) be a white Gaussian noise with two sided PSD 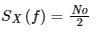
Assume x(t) is input to an LTI system with impulse response h(t) = e-t u(t)
If Y(t) is the output then E[Y2(t)] is ________
A random noise X(t) having a power spectrum

Is applied to a differentiator that has a transfer function H(ω) = jω. The output is applied to a network for which h(t) = t2 e-7t u(t)
The power spectrum of Y(t) is


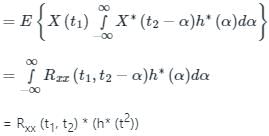
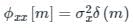
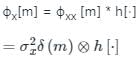
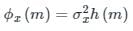
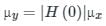
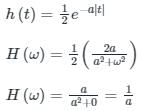


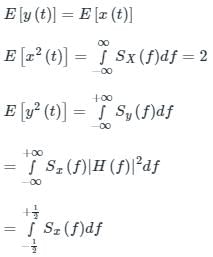
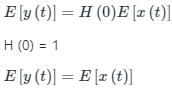
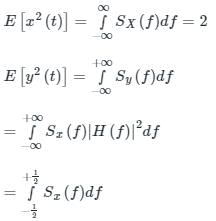
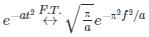
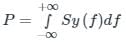

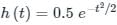
 the Fourier transform is calculated as:
the Fourier transform is calculated as: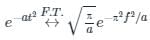
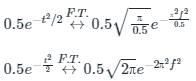

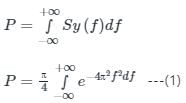
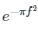 is always equal to 1, i.e.
is always equal to 1, i.e.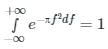
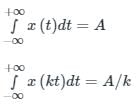
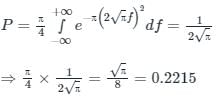
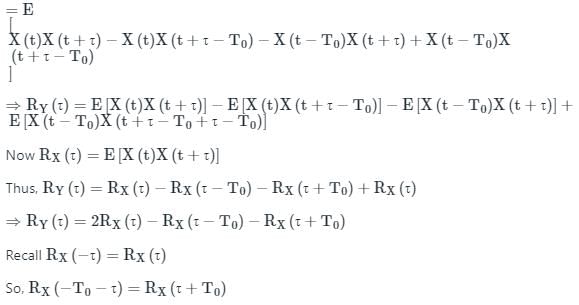

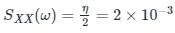 (being the two sided PSD of x(t))
(being the two sided PSD of x(t))