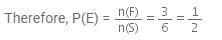Test: Classical Approach to Probability - Class 10 MCQ
15 Questions MCQ Test - Test: Classical Approach to Probability
If the probability of winning a game is 0.995, then the probability of losing is
The probability of an event that is certain to happen is
Which of the following cannot be the probability of an event?
The probability of getting a prime number in single throw of a dice is:
If a die is thrown once, the probability of getting a prime number is
The probability that a non-leap year selected at random will have 53 Mondays is
A card is drawn at random from a pack of 52 playing cards. The probability of getting a face card is
Which one of the following cannot be the probability of an event?
If the probability of winning a game is 0.3, then the probability of losing it is:
If a letter of English alphabet is chosen at random, then the probability that the letter is a consonant is:
If a digit is chosen at random from the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 then the probability that it is odd is
Two coins are tossed together. The probability of getting head on both the coins is
The probability of getting an even number, when a die is thrown once, is:
The probability that a randomly chosen number from one to twelve is a divisor of twelve is