Explore Exams
Login Signup
Sign in Open App
CBSE Class 9  >  Class 9 Test  >  Mathematics (Maths)   >  Test:Triangles- 1 - Class 9 MCQ

Triangles- 1 - Class 9 Maths Free MCQ Test with solutions


MCQ Practice Test & Solutions: Test:Triangles- 1 (25 Questions)

You can prepare effectively for Class 9 Mathematics (Maths) Class 9 with this dedicated MCQ Practice Test (available with solutions) on the important topic of "Test:Triangles- 1". These 25 questions have been designed by the experts with the latest curriculum of Class 9 2026, to help you master the concept.

Test Highlights:

  • - Format: Multiple Choice Questions (MCQ)
  • - Duration: 25 minutes
  • - Number of Questions: 25

Sign up on EduRev for free to attempt this test and track your preparation progress.

Test:Triangles- 1 - Question 1
Save

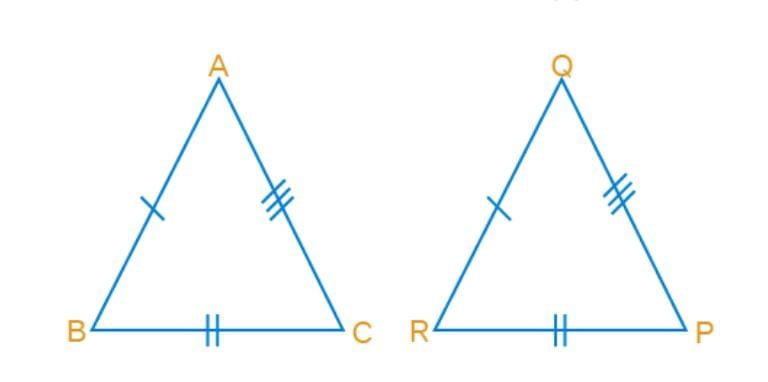
If AB = QR, BC=RP and CA = QP, then which of the following holds?

Detailed Solution: Question 1

- The problem involves two triangles with corresponding side lengths: ( AB = QR ), ( BC = RP ), and ( CA = QP ).
- According to the Side-Side-Side (SSS) Congruence Theorem, two triangles are congruent if all three pairs of corresponding sides are equal.
- To match the sides correctly with the given order, note:
- ( CA = QP )
- ( AB = QR )
- ( BC = RP )
- Therefore, the correct correspondence is △CAB ≅ △PQR

Test:Triangles- 1 - Question 2
Save

△PQR, ∠P = 60∘, ∠Q = 50∘ and Which side of the triangle is the longest?

Detailed Solution: Question 2

Clear all your doubts with EduRev
Test:Triangles- 1 - Question 3
Save

In the adjoining figure, the rule by which △ABC ≅ △ADC

Detailed Solution: Question 3

In the given figure, we need to determine the rule by which ∆ABC is congruent to ∆ADC.

Observations:

  • Side AC: This side is common to both triangles.
  • Side AB = AD: Both sides are 4 cm.
  • Side BC = CD: Both sides are 2.7 cm.

Rule for Congruence:

Since all three corresponding sides of the triangles are equal (AB = AD, BC = CD, AC = AC), the triangles satisfy the Side-Side-Side (SSS) congruence rule.

Correct Answer:

c) SSS

Test:Triangles- 1 - Question 4
Save

In the adjoining figure, BC = AC. If ∠ACD = 115∘, the ∠A is

Detailed Solution: Question 4

In △ABC,
∠ACD+∠ACB = 180∘ (Linear pair)
115∘+∠ACB =180∘
∠ACB = 180∘−115∘=65∘

since AC = BC then ∠ABC = ∠BAC = X
x + x + 65∘ = 180∘
2x = 180∘- 65∘
2x = 115∘
x = 57.5∘

Test:Triangles- 1 - Question 5
Save

If the bisector of the angle A of a △ABC is perpendicular to the base BC of the triangle then the triangle ABC is :

Detailed Solution: Question 5

If the bisector of angle A of a triangle is perpendicular to the base BC of the triangle then the triangle ABC is:

B: Isosceles

Solution:

- The angle bisector of angle A divides the angle into two equal parts.
- For this bisector to be perpendicular to base BC, angles B and C must be equal.
- This means that triangle ABC has two equal sides opposite these equal angles.
- Therefore, triangle ABC is isosceles.

Test:Triangles- 1 - Question 6
Save

Which is true?

Detailed Solution: Question 6

In a triangle, the sum of all three angles must equal 180 degrees.- Option A: If a triangle had two obtuse angles (each greater than 90 degrees), their sum would exceed 180 degrees, which is impossible. Hence, this statement is false. - Option B: A triangle can have two acute angles (each less than 90 degrees). The sum of these two angles will be less than 180 degrees, allowing the third angle to adjust accordingly. This is possible and true.- Option C: If a triangle had two right angles (each exactly 90 degrees), their sum would be 180 degrees, leaving no room for the third angle. Therefore, this statement is false.Thus, only option B is correct.

Test:Triangles- 1 - Question 7
Save

In the adjoining figure, BC = AD, CA⊥AB and BD⊥AB. The rule by which △ABC ≅ △BAD is

Test:Triangles- 1 - Question 8
Save

In the given figure, ABC is an equilateral triangle. The value of x+y is 

Detailed Solution: Question 8

Answer: c) 240°


ABC is an equilateral triangle ⇒ each interior angle is 60°.

At B, x is the exterior angle formed by extending BA beyond B and taking an angle with BC. An exterior angle and its adjacent interior angle form a linear pair, so

x = 180° − ∠ABC = 180° − 60° = 120°.

Similarly at C,

y = 180° − ∠ACB = 180° − 60° = 120°.

Hence,
x + y = 120° + 120° = 240°.

Test:Triangles- 1 - Question 9
Save

In quadrilateral ABCD, BM and DN are drawn perpendiculars to AC such that BM = DN. If BR = 8 cm. then BD is

Test:Triangles- 1 - Question 10
Save

If the altitudes from two vertices of a triangle to the opposite sides are equal, then the triangles is

Detailed Solution: Question 10

Given:

BE = CD

Concept Used:

When 2 sides of a triangle are equal, then it is isosceles.

When 2 angles and 1 side of 2 triangles is equal, then both the triangles are similar.

Calculations:

In △ABE and △ACD,

BE = CD (Given)

∠BEA = ∠CDA (90° each)

∠BAE = ∠CAD (Common Angle)

∠ABE = ∠ACE (By Sum angle property)

⇒ △ABE is similar to △ACD

⇒ AB = AC

∴ If the altitudes from two vertices of a triangle to the opposite sides are equal, then the triangle is isosceles.

Test:Triangles- 1 - Question 11
Save

In △AOC and △XYZ, if ∠A = ∠X, AO = XZ, and AC = XY, then by which congruence rule △AOC ≅ △XZY?

Detailed Solution: Question 11

Given:
∠A = ∠X
AO = XZ
AC = XY

This information satisfies the SAS (Side-Angle-Side) congruence criterion, where two sides and the included angle are equal in both triangles.

Answer: A. SAS

Test:Triangles- 1 - Question 12
Save

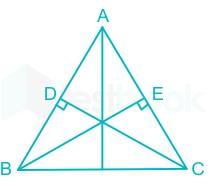
In the adjoining figure, AB = AC and AD⊥BC. The rule by which △ABD ≅ △ACD is

Test:Triangles- 1 - Question 13
Save

In the adjoining Figure, AB = AC and BD = CD. The ratio ∠ABD : ∠ACD is

Detailed Solution: Question 13

Since AB = AC, triangle ABC is isosceles with AB = AC, so angles opposite these sides are equal. Also, BD = CD implies that triangle BDC is isosceles with BD = CD. Point D lies on BC such that BD = CD, making D the midpoint of BC.
Now, consider triangles ABD and ACD:
- AB = AC (given)
- BD = CD (given)
- AD is common to both triangles
Therefore, triangles ABD and ACD are congruent by the Side-Side-Side (SSS) criterion. Corresponding angles of congruent triangles are equal, so ∠ABD = ∠ACD.
Hence, the ratio ∠ABD : ∠ACD = 1 : 1.

Test:Triangles- 1 - Question 14
Save

In △ABC and △PQR, three equality relations between corresponding parts are as follows: AB = QP, ∠B = ∠P BC = PR. State which of the congruence criterion applies in this case:

Detailed Solution: Question 14

Given triangles ABC and PQR with AB = QP, ∠B = ∠P, and BC = PR, we apply the SAS (Side-Angle-Side) congruence criterion. This is because two sides (AB and BC in triangle ABC correspond to QP and PR in triangle PQR) and their included angle (∠B corresponds to ∠P) are equal, satisfying the SAS condition for congruence.

Test:Triangles- 1 - Question 15
Save

O is any point in the interior of △ABC.Then which of the following is true?

Detailed Solution: Question 15

For any point O inside triangle ABC, the sum of distances from O to each vertex (OA + OB + OC) is always greater than half the perimeter of the triangle but less than the full perimeter. This result is supported by geometric inequalities which ensure that OA + OB + OC exceeds 1/2 (AB + BC + CA), making option C correct.

Test:Triangles- 1 - Question 16
Save

It is not possible to construct a triangle when its sides are:

Detailed Solution: Question 16

By the triangle inequality theorem, the sum of any two sides must be greater than the third side.

Option A: 6 cm, 7 cm, 7 cm.

6 + 7 > 7 → 13 > 7 (True). 7 + 7 > 6 → 14 > 6 (True). All three conditions hold, so a triangle is possible.

Option B: 5.4 cm, 2.3 cm, 3 cm.

2.3 + 3 = 5.3, and 5.3 < 5.4, so the sum of these two sides is not greater than the third side. The triangle inequality fails.

Option C: 8.3 cm, 3.4 cm, 6.1 cm.

3.4 + 6.1 = 9.5 > 8.3, and the other pairwise sums also exceed the remaining side, so a triangle is possible.

Option D: 3 cm, 5 cm, 5 cm.

3 + 5 = 8 > 5, and 5 + 5 = 10 > 3, so a triangle is possible.

Therefore, the set that cannot form a triangle is Option B.

Test:Triangles- 1 - Question 17
Save

In the adjoining figure, AB = AC and AD is bisector of ∠A. The rule by which △ABD ≅ △ACD

Test:Triangles- 1 - Question 18
Save

In the adjoining figure, AB⊥BE and FE⊥BE. If AB = FE and BC = DE ,then

Test:Triangles- 1 - Question 19
Save

D,E and f are the mid-points of the sides BC, CA and AB res. Of △ABC. Then △DEF is congruent to triangle:

Detailed Solution: Question 19

When the midpoints of the sides of a triangle are joined, the original triangle is divided into four smaller triangles that are all congruent. In △ABC, D, E, and F are the midpoints of BC, CA, and AB, respectively. Thus, the medial triangle △DEF is congruent to the three other triangles formed:

  • △AFE (with vertices A, F, and E)
  • △FBD (with vertices F, B, and D)
  • △EDC (with vertices E, D, and C)

Since option (a) lists these three triangles, it is the correct answer.

Answer: a) AFE, FBD, EDC

Test:Triangles- 1 - Question 20
Save

Which of the following is not a criterion for congruence of triangles?

Detailed Solution: Question 20

The criteria for congruence of triangles are:

  • RHS: Right Angle-Hypotenuse-Side, which is only used for right triangles 
  • SSS: Side-Side-Side, where all three sides of two triangles are equal
  • SAS: Side-Angle-Side, where two sides and the angle between them are equal
  • ASA: Angle-Side-Angle, where two angles and the included side of one triangle are equal to the corresponding angles and sides of another triangle
  • AAS: Angle-Angle-Side, where two angles and the non-included side of one triangle are congruent to two angles and the non-included side of another triangle

Test:Triangles- 1 - Question 21
Save

△ABC = △PQR, then which of the following is true?

Detailed Solution: Question 21

Triangles ABC and PQR are congruent, meaning their corresponding sides and angles are equal. The correct correspondence based on the given congruency shows that side AC in triangle ABC corresponds to side PR in triangle PQR, making option B accurate.

Test:Triangles- 1 - Question 22
Save

In the adjoining figure, ∠B = ∠C and AD⊥BC. The rule by which △ABD ≅ △ADC

Detailed Solution: Question 22

In the given figure, you can prove that
△ABD ≅ △ADC using either the RHS (Right angle-Hypotenuse-Side) rule or the AAS (Angle-Angle-Side) rule. 

Using the RHS Congruence Rule

The RHS rule applies to right-angled triangles where the hypotenuse and one side are equal in both triangles. In this case:

  • Right Angle: ∠ADB =∠ADC = 90º because AD⟂BC making both triangles right-angled.
  • Hypotenuse (H): Since ∠B=∠C the sides opposite these angles in the larger triangle ABC are equal (AC=AB). These are the hypotenuses of ΔABD and  ΔADC.
  • Side (S): The side AD is common to both triangles.

Therefore,△ABD ≅ △ADC by the RHS rule.

Using the AAS Congruence Rule,

The AAS rule states that two triangles are congruent if two angles and a non-included side of one are equal to the corresponding parts of the other. For this figure:

  • Angle (A): ∠B = ∠C is given.
  • Angle (A): ∠ADB=∠ADC = 90º because AD⟂BC.
  • Side (S): The side AD is a non-included side that is common to both triangles. 

Thus,
△ABD ≅ △ADC is congruent to triangle by the AAS rule. 

Test:Triangles- 1 - Question 23
Save

In the adjoining figure, ABCD is a quadrilateral in which BN and DM are drawn perpendiculars to AC such that BN = DM. If OB = 4 cm. then BD is

Test:Triangles- 1 - Question 24
Save

In triangle PQR length of the side QR is less than twice the length of the side PQ by 2 cm. Length of the side PR exceeds the length of the side PQ by 10 cm. The perimeter is 40 cm. The length of the smallest side of the triangle PQR is :

Detailed Solution: Question 24

Let’s denote the lengths of the sides as follows: Let PQ = x cm. QR = (2x - 2) cm (since QR is less than twice PQ by 2 cm). PR = (x + 10) cm (since PR exceeds PQ by 10 cm). The perimeter of triangle PQR is given as 40 cm: x + (2x - 2) + (x + 10) = 40. Combine like terms: 4x + 8 = 40. Solve for x: 4x = 32. x = 8 cm. Thus, the lengths of the sides are: PQ = 8 cm, QR = (2(8) - 2) = 14 cm, PR = (8 + 10) = 18 cm. The smallest side is PQ with a length of 8 cm.

Test:Triangles- 1 - Question 25
Save

In triangle ABC and triangle DEF, if AB/DE = AC/DF = BC/EF, then the triangles are:

Detailed Solution: Question 25

Explanation: This is the SSS similarity criterion, which states that if the sides of two triangles are in proportion, the triangles are similar

40 videos|468 docs|55 tests
Join Course
Information about Test:Triangles- 1 Page
In this test you can find the Exam questions for Test:Triangles- 1 solved & explained in the simplest way possible. Besides giving Questions and answers for Test:Triangles- 1, EduRev gives you an ample number of Online tests for practice
40 videos|468 docs|55 tests
Join Course
Download as PDF
;

About this Class 9 Practice Test

This test contains 25 MCQs on Test:Triangles- 1 with detailed solutions for each question. It is part of the Mathematics (Maths) Class 9 course on EduRev, designed to align with the current Class 9 syllabus. Each solution explains not just the correct answer but also gives you an understanding of the topic — not just to attempt the question but also help you prepare for the exam with practice.

Explore more Class 9 Study Resources

If you found this Test:Triangles- 1 MCQ Test helpful, you can further enhance your Class 9 preparation with in-depth courses on EduRev, for all the subjects and topics available in Mathematics (Maths) Class 9 course. The course offers:
  • Video Lectures: covering all the topics of Mathematics (Maths) Class 9
  • Notes for Revision: offering revision notes, important questions, summaries, flashcards, cheatsheets & more for Class 9 preparation
  • MCQ Test: variety of questions as per the pattern of Class 9 exam
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup