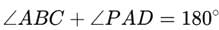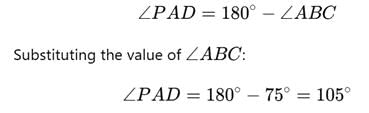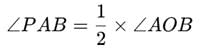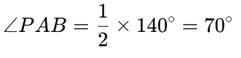Test: Circles- 1 - Grade 9 MCQ
25 Questions MCQ Test - Test: Circles- 1
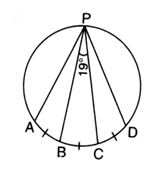
In the given figure, ∠BPC = 19o, arc AB = arc BC = arc CD. Then, the measure of ∠APD is
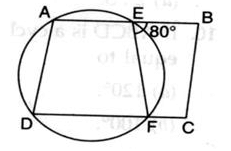
ABCD is a parallelogram. A circle passes through A and D and cuts AB at E and DC at F. If ∠BEF = 80o, then ∠ABC is equal to
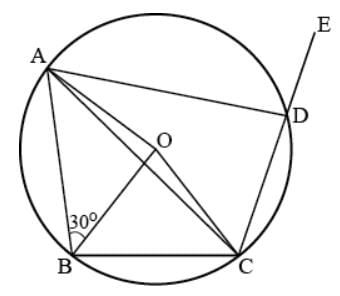
In the given figure, ABCD is a quadrilateral inscribed in circle with centre O. CD is produced to E. If ∠ADE = 95o and ∠OBA = 30o, then ∠OAC is equal to

The given figures show two congruent circles with centre O and O’. Arc AXB subtends an angle of 75o at the centre and arc A’YB’ subtends an angle of 25o at the centre O’. Then, the ratio of arcs AXB to A ‘YB’ is
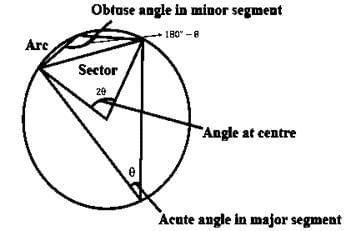
If a chord of a circle is equal to its radius, then the angle subtended by this chord in major segment is
The given figure shows two intersecting circles. If ∠ABC = 75o, then the measure of ∠PAD is
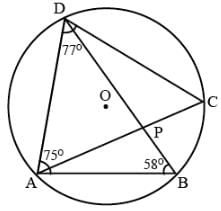
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75o, ∠ABD = 58o and ∠ADC = 77o , AC and BD intersect at P. the measure of ∠DPC is
For what value of x in the figure, points A, B, C and D are concyclic ?
In the given figure PQ and RS are two equal chords of a circle with centre O. OA and OB are perpendiculars on chords PQ and RS, respectively. If ∠AOB = 140o, then ∠PAB is equal to
AD is diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, then the distance of AB from the centre of the circle is
In the given figure, O is the centre of the circle. If ∠CAB = 40o and ∠CBA = 110o, the value of x is :
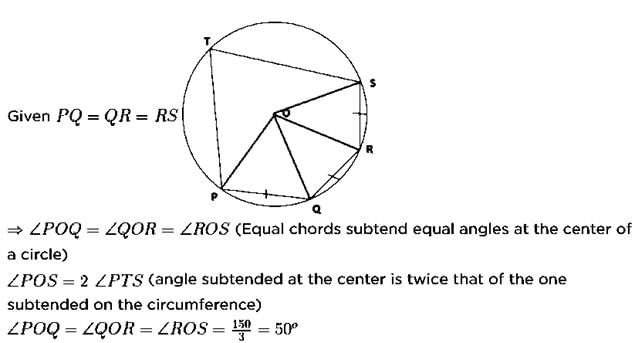
In the given figure PQ = QR = RS and ∠PTS = 75o then the measure of ∠QOR is
In the given figure, O is the centre of the circle ABE is a straight line,. If ∠DBE = 95o then ∠AOD is equal to
The given figure shows two congruent circles with centre O and O’ intersecting at A and B. If ∠AO′B = 50o, then the measure of ∠APB is
Number of circles that can be drawn through three non-collinear points is
In the given figure, if ∠ABC = 50o and ∠BDC = 40o, then ∠BCA is equal to
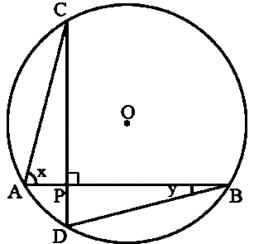
In the given figure, chords AB and CD intersect each other at right angles. Then, ∠x+∠y is equal to
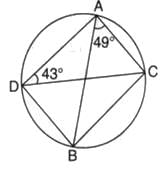
In the given figure if ∠CAB = 49o and ∠ADC = 43o, then the measure of ∠ACB is
In the given figure, O is the centre of the circle. If ∠QPR is 50o, then ∠QOR is :
If TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
In the given figure, O is the centre of a circle. If ∠OAB=40∘ and C is a point on the circle then ∠ACB=?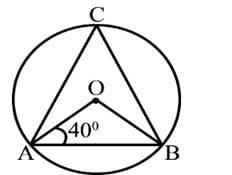
In the given figure, chords AB and CD intersect at P. If ∠DPB=88o and ∠DAP=46o, then the measure of ∠ABC is?