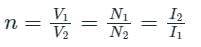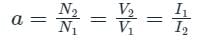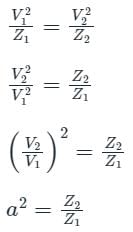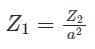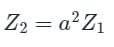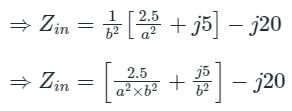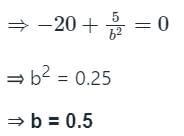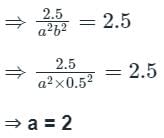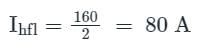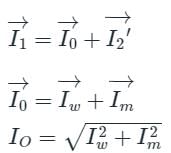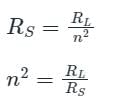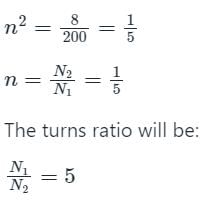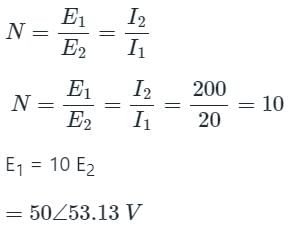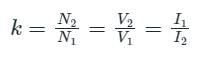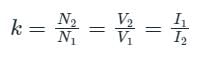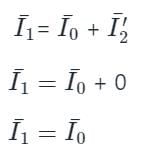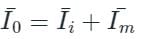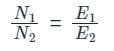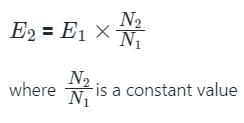Test: Equivalent Circuit of Transformer - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Equivalent Circuit of Transformer
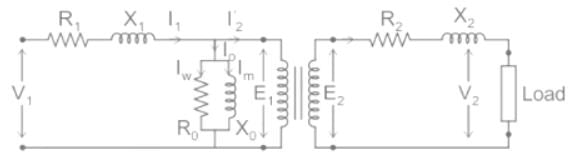
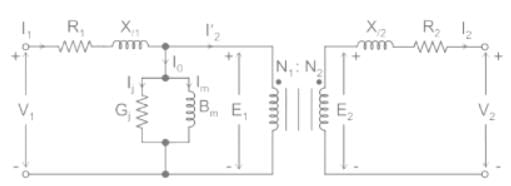
If a 2200/220 V, 60 Hz single phase transformer has primary and secondary resistance of 100 Ω and 10 Ω, respectively. Then the value of equivalent resistance of the transformer referred to the primary side and secondary side are
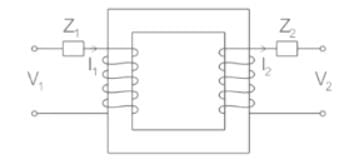
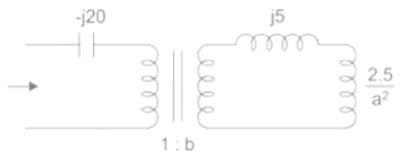
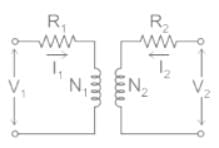
Find the transformer ratios a and b that the impedance Zin is resistive and equal to 2.5 Ω when the network is excited with a sine wave voltage of angular frequency of 5000 rad/s


A one-phase, 50 Hz, 40 kVA transformer with a ratio of 2000 V/250 V has a primary resistance of 1.15 Ω and a secondary resistance of 0.0155 Ω. Calculate total copper loss on half of the full load.
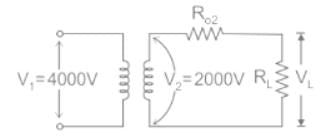
A 4000 V/2000 V, 60 Hz single phase transformer has a total impedance of 60 Ω referred to the primary side. The primary and secondary windings have negligible resistances. If the transformer supplies a resistive of 20 Ω, the full load voltage at the secondary side will be
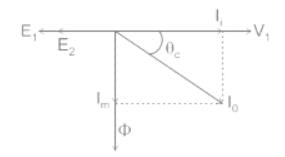
The magnetisation branch of an equivalent circuit of a transformer is drawn in ________ with supply voltage.
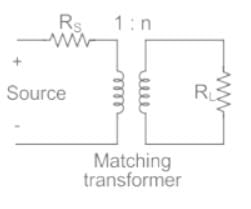
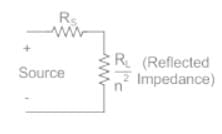
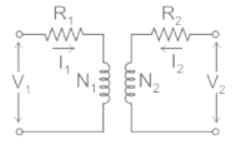
For matching a circuit of output impedance 200 ohms with a load of 8 ohms, the turns ratio of the two winding of transformer should be
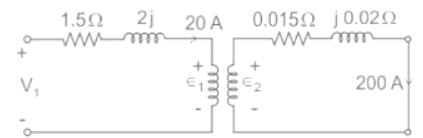
The single phase converter has a full load secondary current of 200 A, while the primary current is one-tenth of this value. Its primary resistance and secondary winding resistances are 1.5 Ω and 0.015 Ω, respectively. The leakage reactance values of the primary and secondary windings are 2 Ω and 0.02 Ω respectively. Which primary voltage will transmit the full load current through a short-circuit secondary, not neglecting the load current?
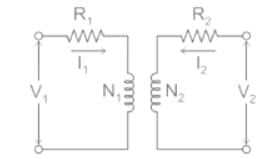
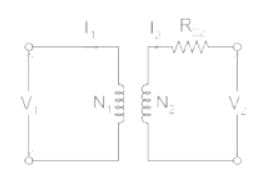
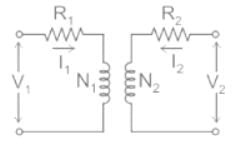
Which of the following is the correct mathematical relationship that connects primary and secondary parameters of a transformer?
Which of the following is the correct mathematical relationship that connects primary and secondary parameters of a transformer?
In a single phase transformer the primary induced and secondary induced voltage vectors are-