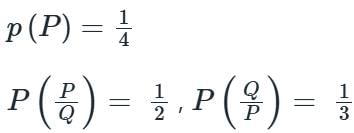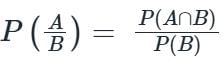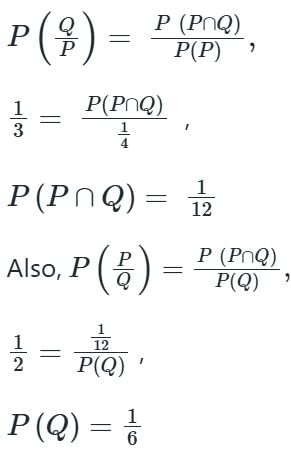Test: Conditional Probability - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Conditional Probability
If P(A) = 5/13, P(B) = 7/13 and P(A∩B) = 3/13, evaluate P(A|B).
If P(A) = 7/11, P(B) = 6 / 11 and P(A∪B) = 8/11, then P(A|B) = ________
Given that E and F are events such that P(E) = 0.5, P(F) = 0.4 and P(E∩F) = 0.3, then what will be the value of P(F|E)?
If P(A) = 1/5, P(B) = 0, then what will be the value of P(A|B)?
Let E and F be events of a sample space S of an experiment, if P(S|F) = P(F|F), then value of P(F|F) is __________
Given that E and F are events such that P(E) = 0.6, P(F) = 0.3 and P(E∩F) = 0.2, then P(E|F) ?
If E and F are two events associated with the same sample space of a random experiment then P (E|F) is given by _________
You have two bags of colored marbles. Bag A contains 3 red marbles and 2 green marbles, while Bag B contains 4 red marbles and 1 green marble. You choose one of the bags at random and then select a marble from that bag. What is the probability that you selected Bag A, given that you picked a red marble?
In a deck of 52 cards, there are 26 red cards (hearts and diamonds) and 26 black cards (spades and clubs). If you draw two cards without replacement, what is the probability that the first card is red and the second card is also red?
P and Q are considering to apply for a job. The probability that P applies for the job is 1/4, the probability that P applies for the job given that Q applies for the job is 1/2, and the probability that Q applies for the job given that P applies for the job is 1/3. Then the probability that P does not apply for the job given that Q does not apply for the job is