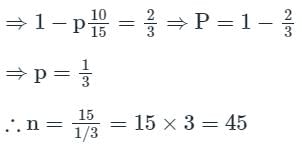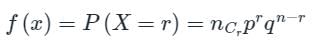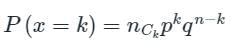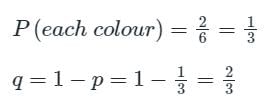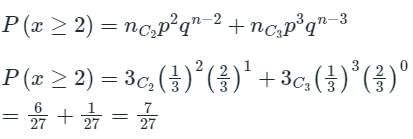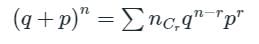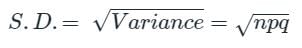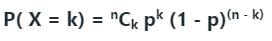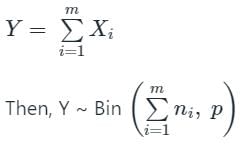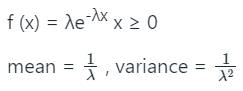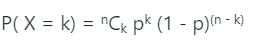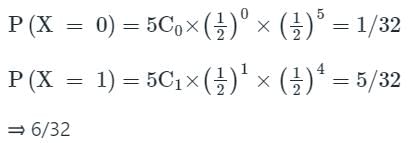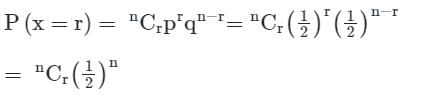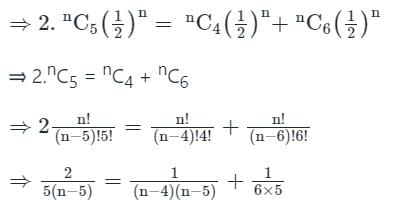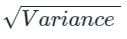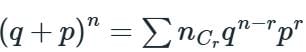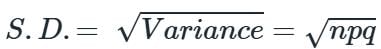Test: Binomial Distribution - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Binomial Distribution
In a Binomial Distribution (BD) the mean is 15 and variance is 10, then parameter n (number of trials) is
The first moment about origin of binomial distribution is
Consider an unbiased cubic dice with opposite faces coloured identically and each face coloured red, blue or green such that each colour appears only two times on the dice. If the dice is thrown thrice, the probability of obtaining red colour on top face of the dice at least twice is _______
Which among the following is the standard deviation of Binomial distribution?
Let X be a random variable that follows Binomial distribution with expectation E(X) = 7 and variance V(X) = 6. Then the probability of success p is
Consider a binomial random variable X. If X1, X2,...Xn are independent and identically distributed samples from the distribution of X with sum 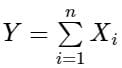 then the distribution of Y as n → ∞ can be approximated as.
then the distribution of Y as n → ∞ can be approximated as.
In an experiment, positive and negative values are equally likely to occur. The probability of obtaining at most one negative value in five trials is
Let x denote the number of times heads occur in n tosses of a fair coin, If P(x = 4), P(x = 5) and P(x = 6) are in AP, then the value of n is
For a given biased coin, the probability that the outcome of a toss is a head is 0.4. This coin is tossed 1,000 times. Let X denote the random variable whose value is the number of times that head appeared in these 1,000 tosses. The standard deviation of X (rounded to 2 decimal places) is _____
Which among the following is the standard deviation of Binomial distribution?