Practice Test for NMAT - 12 - CAT MCQ
30 Questions MCQ Test - Practice Test for NMAT - 12
After selling 70% of the articles on 40% discount shopkeeper announces another 30% discount on the remaining articles. After selling all the articles he makes net profit of 20%. Then find the actual cost price as a ratio of their marked price if the cost price of all articles is equal and so is their marked price?
How many integral values of x satisfy |x + 1| + |x| + |x - 1| + | x - 2| = 7?
Group Question
Answer the following question based on the information given below.
The table below shows the percentage breakup of the fields in which the students that passed from a B-school applied for jobs.
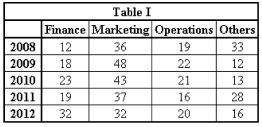
The table below shows the average starting salary for some of these fields.

The graph below shows the number of students that passed out from this B-school in each year. Only students who passed out could apply for jobs, and all of them did so.

Q. If ‘Others’ comprises only Systems and HR, and the number of students applying for HR jobs each year was same what is the least number of students who applied for Systems jobs over the given period?
The table below shows the average starting salary for some of these fields.
The graph below shows the number of students that passed out from this B-school in each year. Only students who passed out could apply for jobs, and all of them did so.
The table below shows the percentage breakup of the fields in which the students that passed from a B-school applied for jobs.
The table below shows the average starting salary for some of these fields.
The graph below shows the number of students that passed out from this B-school in each year. Only students who passed out could apply for jobs, and all of them did so.
Q. In 2009, 25% of the students applying for Marketing jobs applied to Nefertiti, a confectionary major. If only half of them were selected and Nefertiti paid them 10% above the average starting salary, what was Nefertiti’s monthly salary outflow on these recruits?
The table below shows the percentage breakup of the fields in which the students that passed from a B-school applied for jobs.
The table below shows the average starting salary for some of these fields.
The graph below shows the number of students that passed out from this B-school in each year. Only students who passed out could apply for jobs, and all of them did so.
Q. By what percentage did the average salary for this B-school increase from 2010 to 2011?
The table below shows the percentage breakup of the fields in which the students that passed from a B-school applied for jobs.
The table below shows the average starting salary for some of these fields.
The graph below shows the number of students that passed out from this B-school in each year. Only students who passed out could apply for jobs, and all of them did so.
Q. The total amount earned by the students applying for Finance jobs in 2010 was what percent of the total amount earned by the students appyling for Operations jobs in 2012?
A wooden box contains exactly 12 nuts and 24 bolts. One-third of the bolts and one - third of the nuts are defective. If two items are picked from the box up one after the other without replacement, what is the probability that neither item is defective?
MN is a chord of a circle of radius 14 cm. Chord MN subtends a right angle at the center O of the circle. Find the area of the minor segment MCNO, where C is a point on minor arc MN.
Which of the following statements is/are true?
a. A perfect square always has an odd numbers of factors.
b. If a number n has five factors between 1 and the square root of n (n is a perfect square), then n has 13 factors.
c. 72 has 11 factors.
Group Question
Answer the following question based on the information given below.
In a certain country, the movement of the oil and gas industry is dependent on the movement of 3 stocks, A, B and C.
The charts below show the performance of the three stocks over a period of 10 days. X can correspond to any of three stocks, and so can Y.
Q. The oil and gas index of the country is calculated as 3A + 2B + C. The index is said to have ‘Risen’ if all the stocks go up on that day. It is said to be ‘steady’ if 2 stocks go up that day. It is said to be “declining” if only a single stock goes up while it is said to have “plunged” if none of the stocks go up that day.
In a certain country, the movement of the oil and gas industry is dependent on the movement of 3 stocks, A, B and C.
The charts below show the performance of the three stocks over a period of 10 days. X can correspond to any of three stocks, and so can Y.
Q. What is the maximum rise in the value of index from day 1 to day 10?
In a certain country, the movement of the oil and gas industry is dependent on the movement of 3 stocks, A, B and C.
The charts below show the performance of the three stocks over a period of 10 days. X can correspond to any of three stocks, and so can Y.
Q. What is the least possible value of the index?
In a certain country, the movement of the oil and gas industry is dependent on the movement of 3 stocks, A, B and C.
The charts below show the performance of the three stocks over a period of 10 days. X can correspond to any of three stocks, and so can Y.
Q. If the value of the index is 105.5 on day 1, what is its value on day 3?
On Monday, Mohsin increased the speed of car by 25% as compared to his usual speed and reached office 16 minutes earlier. On Tuesday, Mohsin took a longer route to the office and travelled with his usual speed. If on Tuesday, he reached office 20 minutes late, then how many percent more did Mohsin travel to reach office?
A parallelogram with an internal angle of 150° has an area of 48 sq.cm and a perimeter of 40 cm. What is the length of the adjacent sides of the parallelogram (in cm)?
What is the range of x that satisfies the inequality |3x2 - 5| > 5x + 3
Group Question
Answer the following question based on the information given below.
The table below gives the national income and the population of a country for the years 2009-10 to 2014-15.
Q. What was the average of the annual per capita income (in Rs.) over the given eriod?
The table below gives the national income and the population of a country for the years 2009-10 to 2014-15.
Q. What is the difference (in Rs. crore) between the average national income for the given period and the national income for the year having the highest per capita income?
The table below gives the national income and the population of a country for the years 2009-10 to 2014-15.
Q. Which year sees the least percentage growth in the per capita income?
The table below gives the national income and the population of a country for the years 2009-10 to 2014-15.
Q. In 2015-16, the national income and per capita income increased by 25% and 35% respectively. If the population of each year was to be ranked from 1 onwards in ascending order of population, where would 2015-16 be ranked?
A alone can complete some work in 6 days more than what B alone needs to complete it. A started the work and worked alone for 7 days. As soon as he left, B took over and completed the work in 10 more days. In how many days can A and B individually complete the work?
A tank with capacity 84 litres is completely filled with crude oil of purity 70%. Some crude oil is replaced from this tank by cheaper quality oil having 80% impurity. If this decreases the purity of crude oil in the tank by 10 percentage points, how many litres of the cheaper quality oil have been added in the tank?
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
Q. Has Pratap scored more runs than Jagtap at the end of the tournament?
A. Jagtap scores 10 runs more than Pratap in each match they have played together and Pratap has played 10 matches more than Jagtap.
B. Jagtap's average score is 10% more than Pratap and Pratap has played 10% matches more than Jagtap.
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
Q. If the breadth of a rectangle is increased by 2 units and the length is decreased by 3 units, the area is unchanged. What is the area of the rectangle?
A. If the breadth is decreased by 1 unit and the length is increased by 3 units, the area remains the same.
B. If the breadth is increased by 1 unit and the length is increased by 2 units, the area gets doubled.
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
Q. My telephone number is a six-digit number. What is my telephone number?
A. The number is divisible by 22, and three digits of the number are the same.
B. The sum of digits at odd places is equal to 27 and sum of digits at even places is 5. The digits at the hundreds and units place of the number are zero.
Each question is followed by two statements, I and II. Answer each question using the following instructions:
Mark (1) if the question can be answered by using statement I alone but not by using statement II alone.
Mark (2) if the question can be answered by using statement II alone but not by using statement I alone.
Mark (3) if the question can be answered by using either of the statements alone.
Mark (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark (5) if the question cannot be answered by using any of the statements.
Q. How many of the students who had chocolates did not have ice-creams?
I. In a group of 100 students, 75 students either had chocolates or ice-creams or both.
II. Fifty students had both chocolates and ice-creams. The number of students who had only ice-creams is a prime number and the number of students who had only chocolates is also a prime number.
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
Q. What day is today?
A. Hraday went to a movie 10 days ago.
B. Hraday goes to the movie only on a Sunday.
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
Q. Are 2, logy x, logz y and logx z in A.P?
A. x, y and z are in G.P
B. 4 log x = 9 log y, and 4 log y = 10 log z



















