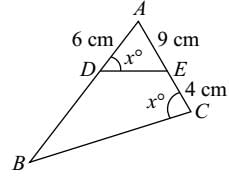
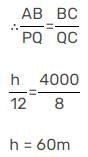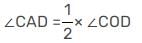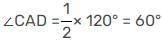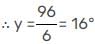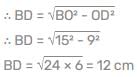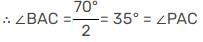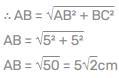MCQ: Geometry - 3 - SSC CGL MCQ
15 Questions MCQ Test - MCQ: Geometry - 3
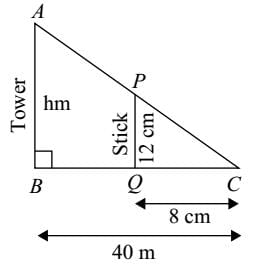
A vertical stick 12 cm long casts a shadow 8 cm long on the ground. At the same time a tower casts the shadow 40 m long on the ground. Find the height of the tower.
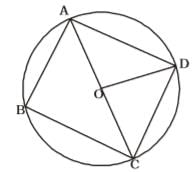
ABCD is a quadrilateral inscribed in a circle with centre O. If ∠COD = 120° and ∠BAC = 30°, then ∠BCD is :
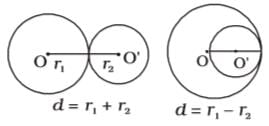
The distance between the centres of the two circles of radii r1 and r2 is d. They will touch each other internally if
If angles of measure (5y + 62°) and (22° + y) are supplementary, then value of y is :
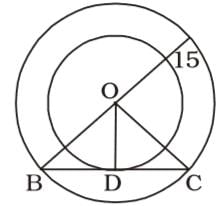
The radius of two concentric circles are 9 cm and 15 cm. If the chord of the greater circle be a tangent to the smaller circle, then the length of that chord is
Two chords AB and CD of a circle with centre O, intersect each other at P. If ∠AOD = 100° and ∠BOC = 70°, then the value of ∠APC is
AB = 8 cm and CD = 6 cm are two parallel chords on the same side of the centre of a circle. The distance between them is 1 cm. The radius of the circle is
If the sum of the interior angles of a regular polygon be 1080°, the number of sides of the polygon is
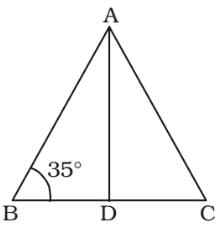
ABC is an isosceles triangle such that AB = AC and ∠B = 35°. AD is the median to the base BC. Then ∠BAD is:
In a triangle, if three altitudes are equal, then the triangle is
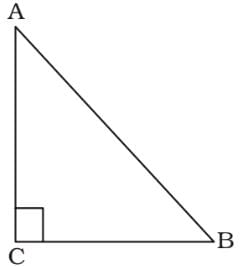
If ∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is :
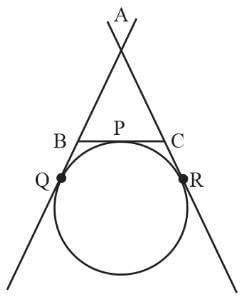
A circle is touching the side BCof Δ ABC at P and is also touching AB and AC produced at Q and R respectively. If AQ = 6 cm, then the perimeter of the triangle ABC is: