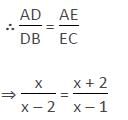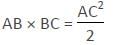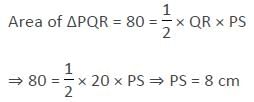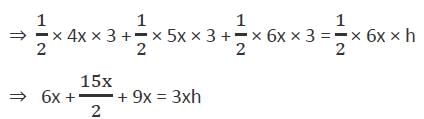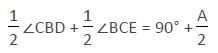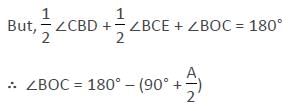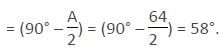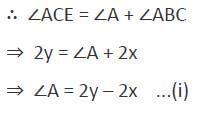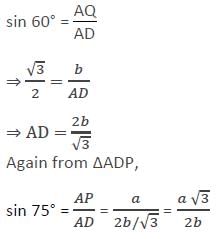MCQ: Triangles - 3 - SSC CGL MCQ
15 Questions MCQ Test - MCQ: Triangles - 3
Directions: Study the following question carefully and choose the right answer:
The sides of a triangle are in the ratio 3 : 4 : 6. The triangle is :
Directions: Study the following question carefully and choose the right answer:
TIf the hypotenuse of a right triangle is 41 cm and the sum of the other two sides is 49 cm, find the difference between the other sides.
Directions: Study the following question carefully and choose the right answer:
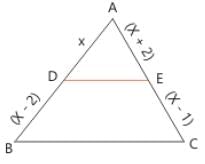
In a Δ ABC, if D and E are the points on the sides AB and AC respectively such that DE || BC and if AD = x , DB = x – 2 , AE = x + 2 and EC = x – 1. then find the value of x .
Directions: Study the following question carefully and choose the right answer:
If the circumcentre of a triangle lies outside it, then the triangle is
Directions: Study the following question carefully and choose the right answer:
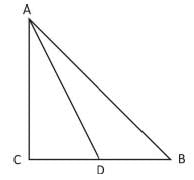
A point D is taken from the side BC of a right-angled triangle ABC, where AB is hypotenuse. Then
Directions: Study the following question carefully and choose the right answer:
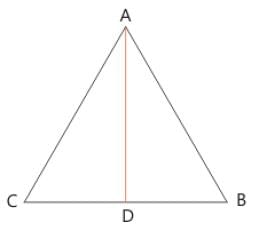
In a equilateral triangle ABC, if AD ⊥ BC, then :
Directions: Study the following question carefully and choose the right answer:
Taking any three of the line segments out of segments of length 2 cm, 3 cm, 5 cm and 6 cm, the number of triangles that can be formed is :
Directions: Study the following question carefully and choose the right answer:
In a right-angled triangle, the product of two sides is equal to half of the square of the third side i.e., hypotenuse. One of the acute angle must be
Directions: Study the following question carefully and choose the right answer:
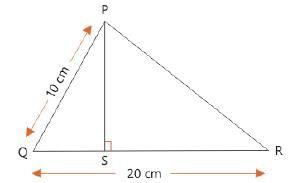
Longest side of a triangle is 20 cm and another side is 10 cm. If area of the triangle is 80 cm2, then what is the length (in cm) of its third side?
Directions: Study the following question carefully and choose the right answer:
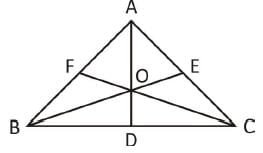
If the length of the sides of a triangle are in the ratio 4 : 5 : 6 and the inradius of the triangle is 3 cm, then the altitude of the triangle corresponding to the largest side as base is :
Directions: Study the following question carefully and choose the right answer:
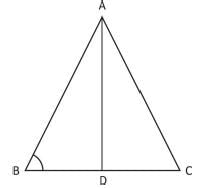
ABC is an isosceles triangle such that AB = AC and AD is the median to the base BC with ∠ABC = 35°. Then ∠BAD is
Directions: Study the following question carefully and choose the right answer:
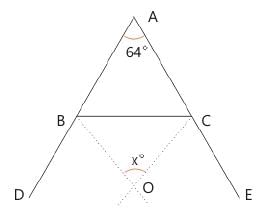
In a Δ ABC, the sides AB and AC have been produced to D and E. Bisectors of ∠CBD and ∠BCE meet at O. If ∠A = 64°, then ∠ BOC is :
Directions: Study the following question carefully and choose the right answer:
ABC is a triangle. The bisectors of the internal angle ∠B and external angle ∠C intersect at D. if ∠BDC = 50°, then ∠A is
Directions: Study the following question carefully and choose the right answer:
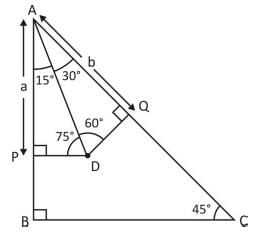
An isosceles triangle ABC is right-angled at B. D is a point inside the triangle ABC. P and Q are the feet of the perpendiculars drawn from D on the side AB and AC respectively of ΔABC. If AP = a cm, AQ = b cm and ∠BAD = 15°, sin 75° = ?
Directions: Study the following question carefully and choose the right answer:
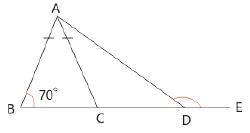
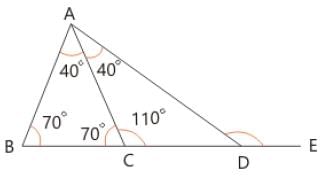
In ΔABC, AB = AC, ∠B = 70°, ∠BAD = 80°, ∠ADE = ?