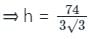MCQ: Right Prism - SSC CGL MCQ
10 Questions MCQ Test - MCQ: Right Prism
The base of a prism is a right-angled isosceles triangle whose hypotenuse is 3√2 cm. If the height of the prism is 12 cm, find the volume of the prism?
A prism has a regular hexagonal base with side 12 cm. If the total surface area of prism is 1024√3 cm2, then what is the height (in cm) of prism?
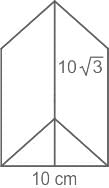
The base of a right prism is an equilateral triangle whose side is 10 cm. If height of this prism is 10√3 cm, then what is the total surface area of prism ?
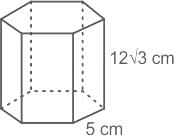
The base of a right prism is a regular hexagon of a side 5 cm. If its height is 12√3 cm, then its volume (in cm3) is:
Find the surface area of a square prism with a 2 cm side and a 4 cm height.
A prism has a regular hexagonal base with side 8 cm and the total surface area of the prism is 912√3 cm2, then what is the height of the prism?
The lateral surface area of a right triangular prism is 288 cm2. If the lengths of the smaller bases are 6 cm and 8 cm respectively, find the height of the prism.
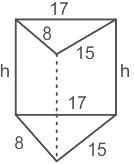
The base of a right prism is a triangle whose sides are 8 cm, 15 cm and 17 cm, and its lateral surface area is 480 cm2. What is the volume (in cm3) of the prism?