GMAT Focus Edition Mock test - 2 - GMAT MCQ
30 Questions MCQ Test - GMAT Focus Edition Mock test - 2
What is the maximum percentage discount that a merchant can offer on her marked price so that she ends up selling at no profit or loss, if she had initially marked her goods up by 50%?
In a class of 40 students, 12 enrolled for both English and German. 22 enrolled for German. If the students of the class enrolled for at least one of the two subjects, then how many students enrolled for only English and not German?
If p > 0, and x2 - 11x + p = 0 has integer roots, how many integer values can 'p' take?
If the average of 5 positive integers is 40 and the difference between the largest and the smallest of these 5 numbers is 10, what is the maximum value possible for the largest of these 5 integers?
There are 6 boxes numbered 1, 2,....6. Each box is to be filled up either with a red or a green ball in such a way that at least 1 box contains a green ball and the boxes containing green balls are consecutively numbered. The total number of ways in which this can be done is ___
How many different positive integers exist between 106 and 107, the sum of whose digits is equal to 2?
The average of 5 consecutive integers starting with m as the first integer is n. What is the average of 9 consecutive integers that start with (m + 2)?
Working together, Jose and Jane can complete an assigned task in 20 days. However, if Jose worked alone and completed half the work and then Jane takes over and completes the second half, the task will be completed in 45 days. How long will Jose take to complete the task if he worked alone? Assume that Jane is more efficient than Jose.
By selling an article at 80% of its marked price, a merchant makes a loss of 12%. What % profit will the merchant make if the article is sold at 95% of its marked price?
If x > 0, how many integer values of (x, y) will satisfy the equation 5x + 4|y| = 55?
If both 112 and 33 are factors of the number a * 43 * 62 * 1311, then what is the smallest possible value of 'a'?
Steve traveled the first 2 hours of his journey at 40 mph and the remaining 3 hours of his journey at 80 mph. What is his average speed for the entire journey?
Sam buys 10 apples for $1. At what price should he sell a dozen apples if he wishes to make a profit of 25%?
x2 + bx + 72 = 0 has two distinct integer roots; how many values are possible for 'b'?
Jane covered a distance of 340 miles between city A and city taking a total of 5 hours. If part of the distance was covered at 60 miles per hour speed and the balance at 80 miles per hour speed, how many hours did she travel at 60 miles per hour?
If the cost price of 20 articles is equal to the selling price of 25 articles, what is the % profit or loss made by the merchant?
y = x2 + bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?
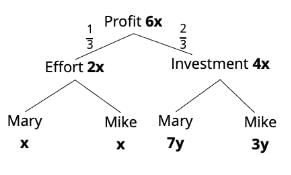
Mary and Mike enter into a partnership by investing $700 and $300 respectively. At the end of one year, they divided their profits such that a third of the profit is divided equally for the efforts they have put into the business and the remaining profit is divided in the ratio of the investments they made in the business. If Mary received $800 more than Mike did, what was the profit made by their business in that year?
For what value of 'm' will the quadratic equation x2 - mx + 4 = 0 have real and equal roots?
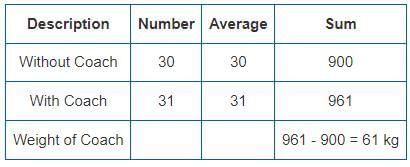
The average weight of a group of 30 friends increases by 1 kg when the weight of their football coach was added. If average weight of the group after including the weight of the football coach is 31 kg, what is the weight of their football coach?
If one of the roots of the quadratic equation x2 + mx + 24 = 0 is 1.5, then what is the value of m?
Five years ago, the town of Bayside, in the Katonic River Valley, had catastrophic flooding one spring, and consequently, most insurers now refuse to write flood insurance for houses in Bayside. The town of Dryadia, in the Phemptic River Valley, is much like Bayside in its proximity to a similar river at an almost identical point in the river valley. We can conclude that the only reason the same insurers do not write flood insurance for houses in Dryadia either is its similarity to Bayside in terms of where it is situated in the river valley.
Q. Which of the following, if true, would most seriously undermine the argument?
Archeologists have discovered three sites showing conclusive evidence for the mastery of fire in Tanzania, from a period slightly after the time that Homo habilis was present in Africa. These sites clearly were founded by Homo erectus, the descendent species of Homo habilis that migrated north, out of Africa and into Asia. Homo erectus was known to have mastered fire, from ample evidence at sites in Asia. There is no reason to attribute mastery of fire to Homo ergaster, the descendent species of Homo habilis that remained in Africa.
Q. Which of the following is an assumption on which the argument depends?
Over the past ten years, the population of Dismaston has grown five times as large as it was. During this time, the average income in the city has risen substantially, and a tremendous amount of capital has flowed into city. An independent audit found that, somewhat surprisingly, the number of violent felonies reported per year is now lower than it was ten years ago.
Q. Each of the following statements below, if true, would explain the somewhat surprising finding EXCEPT:
When, on a particular shopping trip, a consumer purchases an item which he previously had no intention of purchasing, this sale is called an “impulse purchase.” The objects of impulse purchases are occasionally essential items (i.e. items that satisfy basic subsistence needs), but much more frequently are luxury or non-essential items. Researchers have determined that, at the end of a shopping trip, a consumer is much more excited if she has bought a luxury item on an impulse purchase, than if she had made no impulse purchases.
Q. If the information above is true, and if the researchers’ investigation was properly conducted, then which of the following must also be true?
Direction: Read the following Passage and Answer the following Question.
As an instrument of intellectual culture, the study of Physics is profitable to all; as bearing upon special functions, its value, though not so great, is still more tangible. Why, for example, should Members of Parliament be ignorant of the subjects concerning which they are called upon to legislate? In this land of practical physics, why should they be unable to form an independent opinion upon a physical question? Why should the member of a parliamentary committee be left at the mercy of interested disputants when a scientific question is discussed, until he deems the nap a blessing which rescues him from the bewilderments of the committee-room? The education which does not supply the want here referred to, fails in its duty to England.
With regard to our working people, in the ordinary sense of the term ‘working’, the study of Physics would, I imagine, be profitable, not only as a means of intellectual culture, but also as a moral influence to woo them from pursuits which now degrade them. A man's reformation oftener depends upon the indirect, than upon the direct action of the will. The will must be exerted in the choice of employment which shall break the force of temptation by erecting a barrier against it. The drunkard, for example, is in a perilous condition if he contents himself merely with saying, or swearing, that he will avoid strong drink. His thoughts, if not attracted by another force, will revert to the public-house, and to rescue him permanently from this, you must give him an equivalent. By investing the objects of hourly intercourse with an interest which prompts reflection, new enjoyments would be opened to the working man, and every one of these would be a point of force to protect him against temptation.
Q. What is the main purpose of the author in writing the passage?
Direction: Read the following Passage and Answer the following Question.
As an instrument of intellectual culture, the study of Physics is profitable to all; as bearing upon special functions, its value, though not so great, is still more tangible. Why, for example, should Members of Parliament be ignorant of the subjects concerning which they are called upon to legislate? In this land of practical physics, why should they be unable to form an independent opinion upon a physical question? Why should the member of a parliamentary committee be left at the mercy of interested disputants when a scientific question is discussed, until he deems the nap a blessing which rescues him from the bewilderments of the committee-room? The education which does not supply the want here referred to, fails in its duty to England.
With regard to our working people, in the ordinary sense of the term ‘working’, the study of Physics would, I imagine, be profitable, not only as a means of intellectual culture, but also as a moral influence to woo them from pursuits which now degrade them. A man's reformation oftener depends upon the indirect, than upon the direct action of the will. The will must be exerted in the choice of employment which shall break the force of temptation by erecting a barrier against it. The drunkard, for example, is in a perilous condition if he contents himself merely with saying, or swearing, that he will avoid strong drink. His thoughts, if not attracted by another force, will revert to the public-house, and to rescue him permanently from this, you must give him an equivalent. By investing the objects of hourly intercourse with an interest which prompts reflection, new enjoyments would be opened to the working man, and every one of these would be a point of force to protect him against temptation.
Q. Which of the following does the author suggest in the passage about the Members of Parliament?
Direction: Read the following Passage and Answer the following Question.
As an instrument of intellectual culture, the study of Physics is profitable to all; as bearing upon special functions, its value, though not so great, is still more tangible. Why, for example, should Members of Parliament be ignorant of the subjects concerning which they are called upon to legislate? In this land of practical physics, why should they be unable to form an independent opinion upon a physical question? Why should the member of a parliamentary committee be left at the mercy of interested disputants when a scientific question is discussed, until he deems the nap a blessing which rescues him from the bewilderments of the committee-room? The education which does not supply the want here referred to, fails in its duty to England.
With regard to our working people, in the ordinary sense of the term ‘working’, the study of Physics would, I imagine, be profitable, not only as a means of intellectual culture, but also as a moral influence to woo them from pursuits which now degrade them. A man's reformation oftener depends upon the indirect, than upon the direct action of the will. The will must be exerted in the choice of employment which shall break the force of temptation by erecting a barrier against it. The drunkard, for example, is in a perilous condition if he contents himself merely with saying, or swearing, that he will avoid strong drink. His thoughts, if not attracted by another force, will revert to the public-house, and to rescue him permanently from this, you must give him an equivalent. By investing the objects of hourly intercourse with an interest which prompts reflection, new enjoyments would be opened to the working man, and every one of these would be a point of force to protect him against temptation.
Q. Each of the following can be inferred from the information in the passage EXCEPT?
During medieval times, the administrative system was organized such that jobs were traditionally held within the same family. The eldest son of the village's blacksmith will take up his father's business and become the next blacksmith. The other sons would join the army or serve the king in some fashion while the daughters did what their mother did. Although the world has undergone innumerable changes, the dynastic system has not undergone any change whatsoever. Children who have fathers who played major league baseball are 800 times more likely than other kids to become major league players themselves.
Q. Which of the following best refutes the author's reasoning?
A survey conducted recently in the city indicated that most college welfare-aid applicants understate the number of luxury items - such as cars and TVs - that their family owned, in an effort to maximize the amount of aid they can claim from the city. Paradoxically, the same study also found that many applicants claimed that they had running water and a gas connection even when they did not.
Q. Which of the following best explains the apparent paradox?


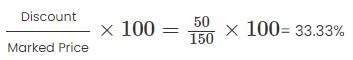

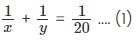
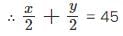
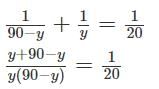
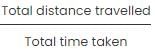

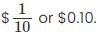
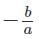 represents the sum of the roots of the quadratic equation and c/a represents the product of the roots of the quadratic equation.
represents the sum of the roots of the quadratic equation and c/a represents the product of the roots of the quadratic equation.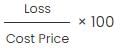
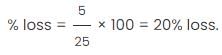
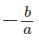
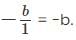
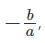 , and product of the roots, αβ = c/a.
, and product of the roots, αβ = c/a.















