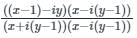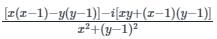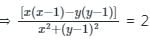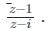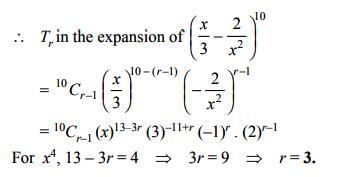NDA Mock Test: Mathematics - 2 - NDA MCQ
30 Questions MCQ Test - NDA Mock Test: Mathematics - 2
Let R be a relation defined as R = {(x, y): y = 2x, x is natural number < 5} then Range of R is given as ,
A relation R defined on the set A = {1, 2, 3, 5} as {(x, y): x + y >10 : x, y ∈ A} is:
If a > 0 and discriminant of ax2+2bx+c is –ve, then

If the system of linear equations
x + 2ay +az = 0 ; x +3by+bz = 0 ; x +4cy+cz = 0 ; has a non - zero solution, then a, b, c.
Points (a,a,c),(1,0,1) and (c,c,b) are collinear if
If A is a square matrix of order 3 and |A| = 7 then |AT| =
If |z1| = 4, |z2| = 4, then |z1 + z2 + 3 + 4i| is less than
If A = 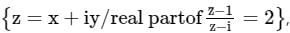 then the locus of the point P(x, y) in the cartesian plane is
then the locus of the point P(x, y) in the cartesian plane is
Among 7 flags 4 are of red colour and the rest are all different colours. How mant different signals can be generated using these flags?
If n is a +ve integer, then the binomial coefficients equidistant from the beginning and the end in the expansion of (x+a)n are
If the rth term in the expansion of 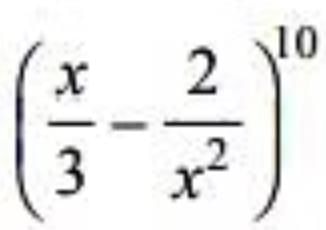 contains x4, then r =
contains x4, then r =
A sequence a1, a2, a3,…, an is called ______ progression, if each term is non-zero and 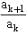 = constant for
= constant for
Which of the following sequeces in GP will have common ratio 3,where n is an Integer?
If the third term of an A.P. is 7 and its 7th term is 2 more than three times of its 3rd term, then sum of its first 20 terms is-
[AIEEE- 2002]
If x1, x2, x3 and y1, y2, y3 are both in G.P. with the same common ratio, then the points (x1, y1), (x2, y2) and (x3, y3)
[AIEEE- 2003]
The line through the points (a , b) and (- a, - b) passes through the point
Which of the following lines is parallel to the line with equation 2x+y=3?
The equation of the line having normal distance 2a from the origin and angle 60° which the normal makes with the positive direction of X-axis is:
The radius of the circle passing through the foci of the ellipse 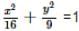 and having its centre at (0, 3) is
and having its centre at (0, 3) is
The line y = c is a tangent to the parabola 7/2 if c is equal to
The equation of the circle passing through (0, 0) and making intercepts 2 and 4 on the coordinate axes is:



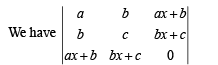
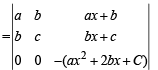
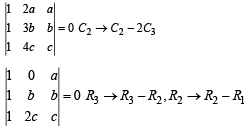
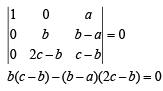
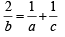
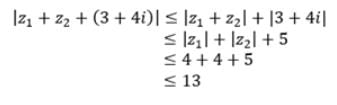
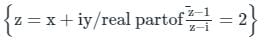
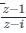 = Real Part of
= Real Part of 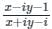 = Real Part of
= Real Part of