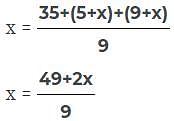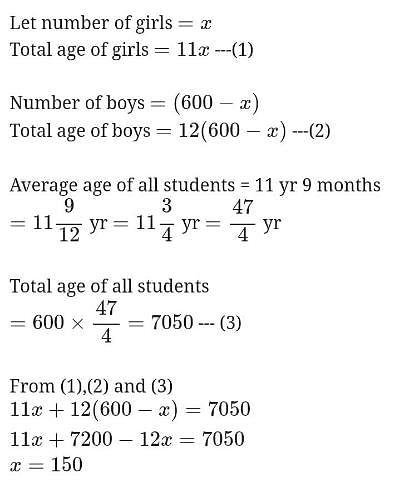Test: Average- 2 - CLAT MCQ
20 Questions MCQ Test - Test: Average- 2
If the sum of five consecutive odd numbers is 255 then find the sum of largest and smallest number.
Nine students of a class contribute a certain sum. Seven of them give Rs. 5 each and the other two give Rs. 5 & 9 more then the average contribution of all the 9 students. The average contribution of the class of 9 students is.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Sonam calculates average of 10 positive 2 digit integers. By mistake she interchanges the digits of one number while calculating the average. Because of which, the average becomes 2.7 less than the correct answer. What is the difference between the two digits of the number which was reversed while calculating the average?
There are total 600 students in a school. Average age of boys is 12 years and of girls is 11 years while average age of all students is 11 yrs. And 9 months. Find the number of girls in the school.
Ratio between present ages of A, B and C is 5:4:6. Total of the ages of A and C after 5 years will be 54 years. What will be the ratio of ages of B and C after 4 years?
A farmer wants to mix 100 kg of Rs. 40/kg rice and some quantity of Rs. 60/kg rice. What quantity of 60kg rice should be mixed to get Rs. 50 /kg rice mix?
Sum of the ages of a father and son is 45 years. Five years, ago product of their ages was 4 times the father’s age at that time. Present ages of father and his son, respectively are:
Kamla got married 6 years ago. Today her age is 1(1/4) times her age at the time of marriage. Her son age is 1/10 times her age. Her son age is:
John inherits Rs. 200000, and invests a part of money in bonds with an interest rate of 11% per annum, and saves the remainder at 9% per annum. He receives Rs. 20400 as interest for 1 year. What amount he invested at 11% and 9 % respectively?
Ratio of father’s age to his son’s age is 7:3. Product of their ages is 756. Ratio of their ages after 6 years will be
The ratio of Vipan’s age & Sonia’s age is 3:5 and the sum of their age is 80 years. The ratio of their ages after 10 years will be.
Average of five numbers is 15 while average of three of those numbers is 11. Find the average of remaining two numbers.
The age of father is 5 times that of his son. 3 years ago, the age of father was 8 times that of his son. Find the present age of father.
A cricketer has completed 10 innings and his average is 21.5 runs. How many runs must he make in his next innings so as raise his average to 24?
The ratio of father’s age to the son’s age is 4:1 the product of their ages is 196. What will be the ratio of their ages after 5 years?
The ratio of the ages of father and the son at present is 6:1. After 5 years the ratio will become 7:2. What is present age of the son?
After 5 years, the age of father will be thrice the age of his son, whereas five years ago he was 7 times as old as his son was. What is the present age of father?
The ratio of the age of Rahul five years before to the age of Shiv 5 years hence is 3 : 5 and the ratio of the present age of Rahul to the present age of Riya is 5 : 4. If the average present age of Shiv and Riya is 18 years, then the present age of Riya is?
The average age of a board of 10 consultants of a firm is same as it was 2 yrs back on account of the replacement of one of the older consultants by a younger man. Find the difference between the age of the old consultant and the young man.
The average age of a group of 10 students was 20. The average age increased by 2 years when two new students joined the group. What is the average age of the two new students who joined the group?