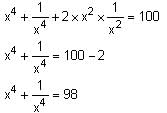MAHA TET Paper 1: Mathematics Test - 4 - MAHA TET MCQ
30 Questions MCQ Test - MAHA TET Paper 1: Mathematics Test - 4
Examine the following matchstick patterns.
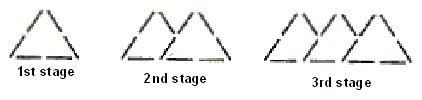
If the pattern continues, how many matchsticks are needed in the 15th stage?
If the pattern continues, how many matchsticks are needed in the 15th stage?
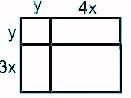
Which of the following expression represents the area of the rectangle given below?

The teaching methodology of Maths has become quite old and as a result, the students are lacking interest in the subject. Therefore, modernisation in training of mathematics can be branched out in terms of
While teaching the addition of fractions, it was observed by Mr. Singh that the following type of error is very common:
2/3 + 2/5 = 4/10
Mr. Singh should take the following remedial action:
Identify the incorrect statement from among the following:
In order to understand students' difficulty in understanding mathematics and their point of view, the teacher must understand the point of view of the students. Therefore, to teach mathematical content effectively, teachers need a fundamental understanding of
When 121012 is divided by 12, the remainder is_____.
Which of the following is true about brainstorming?
i. It helps to achieve the higher order of cognitive objectives.
ii. It helps as a democratic technique of teaching.
iii. It provides more ideas and views to the child.
Look at the following table:

Which bus takes the least time to reach Mathura from New Delhi?
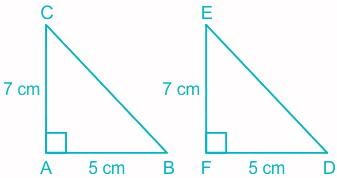
In ΔABC and Δ DEF, AB = 5 cm, AC = 7 cm, ∠A = 90°, FD = 5 cm, EF = 7 cm and ∠F = 90°. Then,
The purpose of a diagnostic test in mathematics is:
Procedural fluency in Mathematics implies knowledge of rules, formulae, or algorithms, and implementing them with accuracy, flexibility and efficiency:
Flexibility in Mathematics refers to:
The table shows the number of students of a school who play different games.
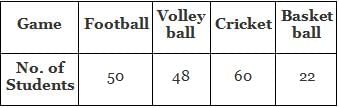
When the data shown in the table above is presented in a pie chart, what will be the measure of the central angle of the sector representing the students playing Volley Ball?
A teacher introduced multiplication in her class as repeated addition. Then, by grouping of same number of objects taken multiple times, she introduced the 'x' symbol. Further, she conducted a small activity of finding product using criss-cross lines of matchsticks. Here, the teacher is
To be a "good" mathematician one must be able to:
The human information processing system does not have which of the following features which have very direct implications for introducing young children to the world of formal mathematics
If x2 + 1/x2 = 10, then the value of x4 + 1/x4 is
Study the following patterns
1 x 1 = 1
11 x 11 = 121
111 × 111 = 12321
.....
....
What is 11111 × 11111 = ?
Find the missing term in the following series:
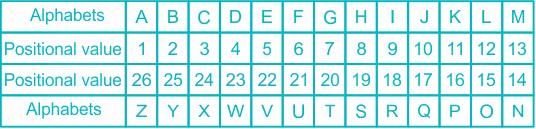
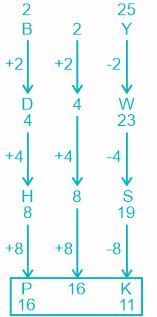
B2Y, D4W, H8S, ______
What is the role of memory in learning mathematics?
"Which two numbers when multiplied gives the product 24?" This question _____.
Consider the frequency distribution table the classification of marks obtained by 40 students out of 36 marks in mathematics test.
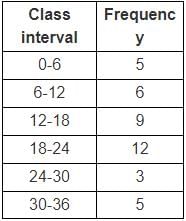
How many students got marks between 12 to 24?
Arjun, a student of IV, is able to answer all the questions related to Number System orally, but commits mistakes while writing the solutions of problems based on Number System. The best remedial strategy to remove errors in his writing is
A rhombus has diagonals of length 8 cm and 6 cm. Find its perimeter:
Rizul is a kinesthetic learner. His teacher Ms. Neha understood his style of learning. Which of the following strategies should she choose to clear his concept of multiplication?
Which method was used in the below solution?
Given:
b/a = d/c
To prove: d(c - 2b) = d (a - 2ab) = b(c - 2ad)
Solution: d(a - 2ab) = b(c - 2ad)
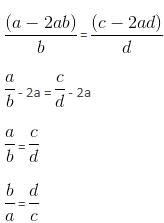
Which of the following cannot be considered as a reason for fear and failure in mathematics?