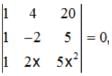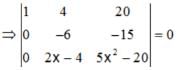Test: Matrices & Determinants(May 7) - JEE MCQ
15 Questions MCQ Test - Test: Matrices & Determinants(May 7)
If A and B are any two square matrices of the same order, then
The transformation ‘orthogonal projection on X-axis’ is given by the matrix
The equations x + 2y + 2z = 1 and 2x + 4 y + 4z = 9 have
The number of all the possible matrices of order 2 × 2 with each entry 0, 1 or 2 is
A square matrix A = [aij]n×n is called an upper triangular if aij = 0 for
The equations, x + 4 y – 2 z = 3, 3 x + y + 5 z = 7, 2 x + 3y +z = 5 have
If the system of equationsx + 4 ay + az = 0, x + 3by + bz = 0 andx + 2 cy +cz = 0 have a non-zero solution,then a, b, c are in
If I3 is the identity matrix of order 3 , then 13−1 is
If A and B are square matrices of same order and A’ denotes the transpose of A , then
A square matrix A is invertible iff det A is equal to
If the entries in a 3 x 3 determinant are either 0 or 1 , then the greatest value of this determinant is :
In a third order determinant, each element of the first column consists of sum of two terms, each element of the second column consists of sum of three terms and each element of the third column consists of sum of four terms. Then it can be decomposed into n determinants, where n has value




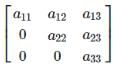 .
.
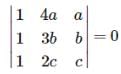
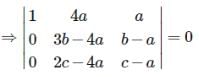
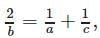 ∴ there, a , b ,c, are in H.P
∴ there, a , b ,c, are in H.P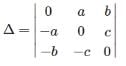

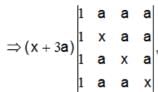
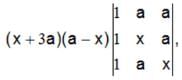
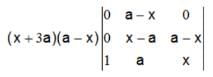
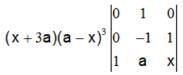


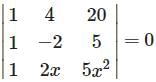 are
are