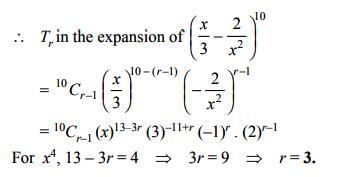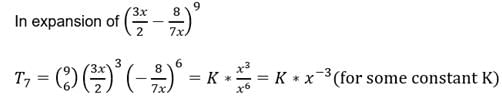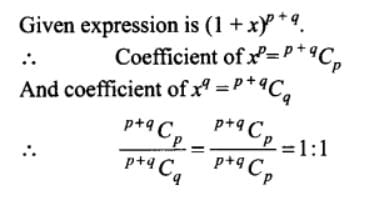Test: Binomial Theorem: Simple Applications (May 30) - JEE MCQ
10 Questions MCQ Test - Test: Binomial Theorem: Simple Applications (May 30)
If n is a +ve integer, then the binomial coefficients equidistant from the beginning and the end in the expansion of (x+a)n are
If the rth term in the expansion of 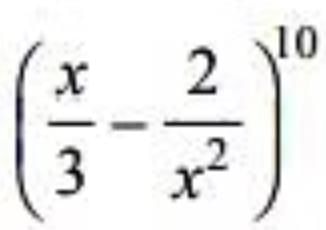 contains x4, then r =
contains x4, then r =
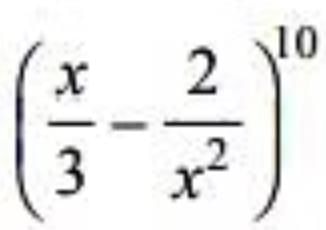 contains x4, then r =
contains x4, then r =If the coefficients of x−7 and x−8 in the expansion of 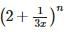 are equal then n =
are equal then n =
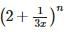 are equal then n =
are equal then n =The largest term in the expansion of (1+x)19 when x = 1/2 is
If coefficients of three successive terms in the expansion of (x+1)n are in the ratio 1 : 3 : 5, then n is equal to
The exponent of power of x occurring in the 7th term of expansion of
The term independent of x in the expansion of
The number of dissimilar terms in the expansion of (a+b)n is n + 1, therefore number of dissimilar terms in the expansion of (a+b+c)12 is
The term containing x3 in the expansion of (x−2y)7 is
The coefficients of xp and xq (p, q are + ve integers) in the binomial expansion of (1+x)p+q are