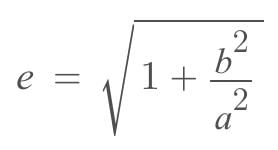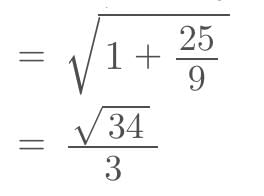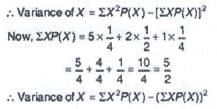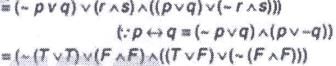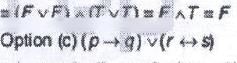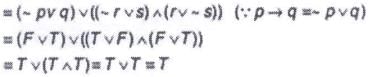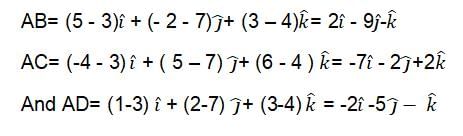AP EAMCET Mock Test - 1 - JEE MCQ
30 Questions MCQ Test - AP EAMCET Mock Test - 1
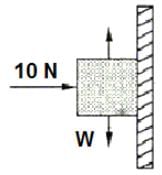
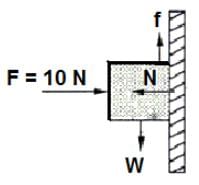
A horizontal force of 10 N is necessary to hold a stationary block against a wall. The coefficient of friction between the block and the wall is 0.2. The weight of the block is

Two blocks of masses m and M are placed on a horizontal frictionless table connected by a spring as shown in the figure. The block of mass M is pulled to the right with a force F. If the acceleration of the block of mass m is 'a', then the acceleration of the block of mass M will be


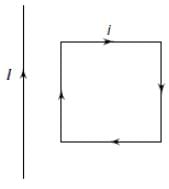
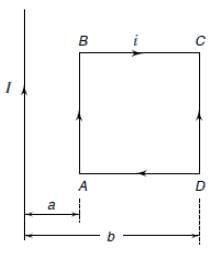
A rectangular loop carrying a current i is situated near a long straight wire such that the wire is parallel to one of the sides of the loop. If a steady current is established in the wire, as shown in the figure, the loop will

The angular momentum of the Earth revolving around the Sun is proportional to Rn, where R is the distance between the Earth and the Sun. The value of n is
Spot the wrong statement:
The acceleration due to gravity g decreases if,
In a certain double slit experimental arrangement, interference fringes of width 1.0 mm each are observed when light of wavelength 5000 Å is used. Keeping the set-up unaltered if the source is replaced by another wavelength of 6000 Å, the fringe width will be -
A radioactive sample S1 having an activity of 5 μCi has twice the number of nuclei as another sample S2, which has an activity of 10μCi The half lives of S1 and S2 can be
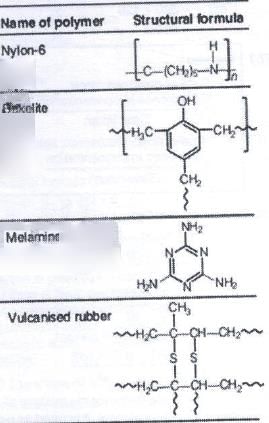
Which among the following polymer does not show cross linking in it?
Based on first Jaw of thermodynamics which of the following is correct
The molar conductivities at infinite dilution for sodium acetate, NaAc, HCI and NaCI are 91 S cm2 mol-1, 425.9 S cm2 mol-1 and 126.4 S cm2 mol-1 respectively. The molar conductivity of acetic acid at infinite dilution is
A particle moves so that x = 2 + 27t - t3. The Erection of motion reverses after moving a distance of ... units.
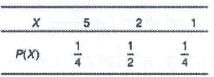
A player tosses 2 fair coins. He wins Rs. 5 if 2 heads appear, Rs. 2 If 1 head appear and Rs. 1 if no head appears, then the variance of his winning amount is
If the sum of the slopes of the lines given by x² – 4p x y + 8y² = 0 is three times their product, then p =
If p and q are true and r and s are false statements, then which of the following is true?
If f( x) = (x), where (x) is the greatest integer not greater than x, then f’(1) = ...
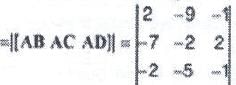
If A, B, C and D are (3, 7, 4), (5, -2, 3), (-4, 5, 6) and (1, 2, 3) respectively, then the volume of the parallelepiped with AB, AC and AD as the coterminous edges, is ....... cubic units.
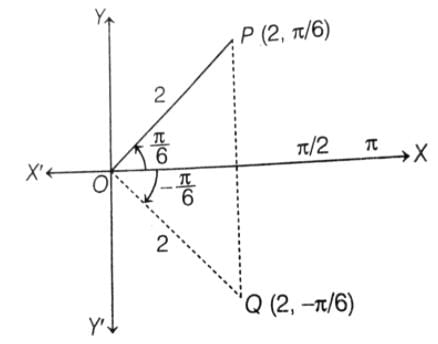
The polar coordinatesThus, if of P are(2, π/6). If Q is the image of P about the X-axis, then the polar coordinates of Q are......
Let X be the number of successes in 'n' independent Bernoulli trials with probability of success p = ¾, The least value of ‘n’ so that P(X ≥ 1) ≥ 0.9375 is .......
For any non zero vector, a,b,c
a.[(b + c) x (a + b + c)] = ...




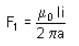
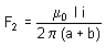


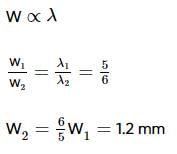
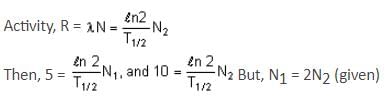
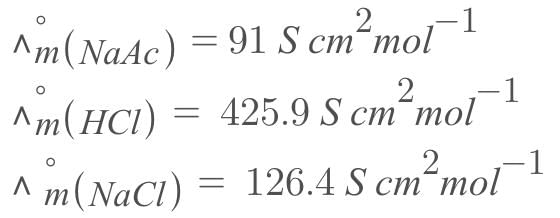

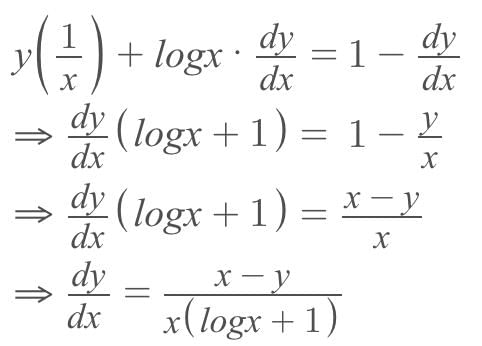
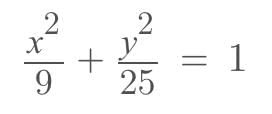
 we get
we get