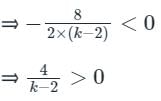Test: Quadratic Equations: Nature of Roots (June 8) - JEE MCQ
10 Questions MCQ Test - Test: Quadratic Equations: Nature of Roots (June 8)
If f(x) = 3x2 - 5x + p and f(0) and f(1) are opposite in sign, then which of the following is correct?
The value of k for which the equation (k - 2)x2 + 8x + k + 4 = 0 has both real, distinct and negative roots is
If the roots of the equation x2 - ax - bx - cx + bc + ca = 0 are equal, then which one of the following is correct?
Consider the following statements in respect of the roots of the equation x3 - 8 = 0:
- The roots are non-collinear.
- The roots lie on a circle of unit radius.
Which of the above statements is/are correct?
The equation px2 + qx + r = 0 (where p, q, r all are positive) has distinct real roots a and b. Which one of the following is correct?
Determine the nature of the roots of the equation 2x2 + 5x + 5 = 0
If α and β are the roots of the equation x2 - px + q = 0, then ∑(α2 + β2) is
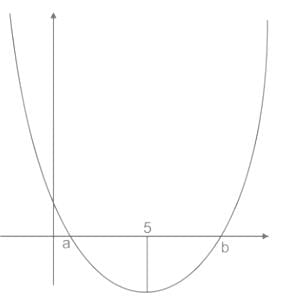
If 5 lies between the roots of the quadratic equation x2 + 2(k - 3)x + 9 = 0, find the complete solution set of k.
It is given that the roots of the equation x2 – 2x – log2 K = 0 are real. For this, the minimum value of K is
If the equation x2 - (2 + m)x + (m2 - 4m + 4) = 0 in x has equal roots, then the values of m as