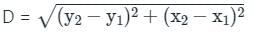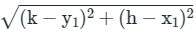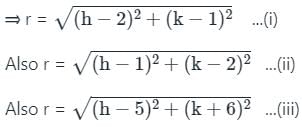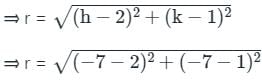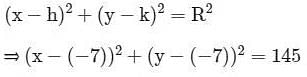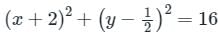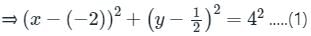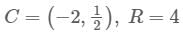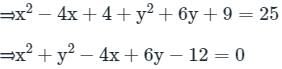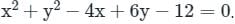Test: Circles: Equation of a Circle (8 July) - JEE MCQ
10 Questions MCQ Test - Test: Circles: Equation of a Circle (8 July)
Find the equation of a circle whose end points of any diameter are (2, −1) and (−2, 2).
The equation of the circle passing through (4, 5) having the centre at (2, 2) is
Find the equation of circle passing through (1, 2), (2, 1) and (5, -6)
Find the center and radius of the equation 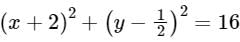
Find the equation of a circle whose centre is (−3, 2) and area is 176 units2 .
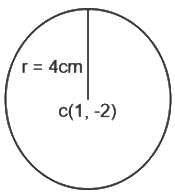
The equation of circle with centre (1, -2) and radius 4 cm is:
Find the equation of a circle, if the end points of the diameters are A (3, 2) and B (2, 5) ?
Find the equation of the circle whose center is (2, -3) and radius is 5.
Find the equation of a circle with centre at (2, - 3) and radius 5 units.
Find the equation of a circle whose centre is (2, - 1) and which passes through the point (3, 6) ?