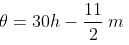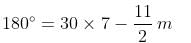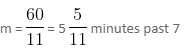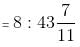Test Level 2: Clocks & Calendars - 2 (August 21) - CAT MCQ
10 Questions MCQ Test - Test Level 2: Clocks & Calendars - 2 (August 21)
At what time between 5 and 6 o'clock will the hands of a clock be 3 minutes apart?
In the year 1648, if February had 5 Sundays, then what was the day on February 13, 1750?
At what time between 4 o'clock and 5 o'clock will the hands of a clock be at a right angle?
At what time between 4:15 a.m. and 5:05 a.m. will the angle between the hour hand and the minute hand of a clock be the same as the angle between the hands at 8:45 p.m.?
Alex turned a clock on at 3:00 pm. But the clock is defective, due to which it lags behind by 9 minutes after each day (24 hours). What will be the real time when the clock indicates 6:00 am on the 4th day of it's successive working?
If 15th March, 2013 was a Friday, then 10th July, 2013 will be a
At what time between 7 o'clock and 8 o'clock will the hands of a clock be in a straight line but not together?
How many days will there be from 23rd January, 2011 to 31st July, 2013 (both days included)?
Two clocks are set correctly at 10 a.m. on Friday. The first clock gains 2 minutes per hour, which is twice as much as gained by the second clock. What time will the second clock register when the correct time is 2 p.m. on the following Monday?
A man went outside between 7 o'clock and 9 o'clock at such a time that the minute hand and the hour hand were found to be coinciding before 8 o'clock; and when he returned, again he found both the hands to be coinciding, but after 8 o'clock. What was the time when he returned to the house?


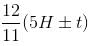
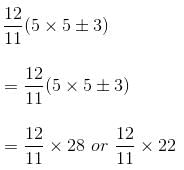
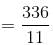 mins or 24 mins
mins or 24 mins
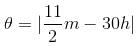 [where θ = angle between the hour-hand and the minute-hand, m - minutes, h - hours]
[where θ = angle between the hour-hand and the minute-hand, m - minutes, h - hours]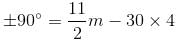
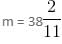 minutes past 4 or m =
minutes past 4 or m = 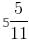 minutes past 4.
minutes past 4.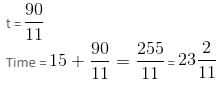
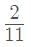 minutes past 4 o'clock
minutes past 4 o'clock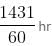 on this clock = 24 hr on the correct clock
on this clock = 24 hr on the correct clock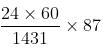 hr on the correct clock
hr on the correct clock