Moles removed = 18.2 – 14.54
= 3.656 moles
Mass removed = 3.656 × 32 = 116.99 g = 0.116 kg
Three vessels of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monatomic), the second contains chlorine (diatomic), and the third contains uranium hexafluoride (polyatomic). The number of molecules
One mole of an ideal monatomic gas is at an initial temperature of 300 K. The gas undergoes an isovolumetric process, acquiring 500 J of energy by heat. It then undergoes an isobaric process, losing this same amount of energy by heat. Determine the new temperature of the gas
Calculate the change in internal energy of 3.00 mol of helium gas when its temperature is increased by 2.00 K.
One mole of an ideal monatomic gas is at an initial temperature of 300 K. The gas undergoes an isovolumetric process, acquiring 500 J of energy by heat. It then undergoes an isobaric process, losing this same amount of energy by heat. Determine the work done on the gas.
1 mole of a monoatomic gas is mixed with 3 moles of a diatomic gas. What is the molecular specific heat of the mixture at constant volume?
One mole of hydrogen gas is heated at constant pressure from 300 K to 420 K. Calculate the energy transferred by heat to the gas
One mole of hydrogen gas is heated at constant pressure from 300 K to 420 K. Calculate the increase in its internal energy.
Two moles of an ideal gas (γ=1.4) expands slowly and adiabatically from a pressure of 5.00 atm and a volume of 12.0 L to a final volume of 30.0 L. What is the final pressure of the gas?
The average distance a molecule can travel without colliding is called the
According to Atomic Hypothesis: little particles of atom
In dynamic equilibrium, molecules collide and change their speeds during the collision
One mole of hydrogen gas is heated at constant pressure from 300 K to 420 K. Calculate the work done by the gas.
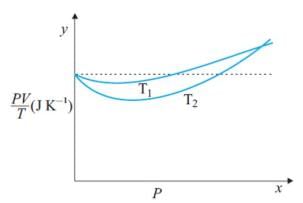
Figure shows plot of PV/T versus P for 1.00x10-3 kg of oxygen gas at two different temperatures. What is the value of PV/T where the curves meet on the y-axis?
Nine particles have speeds of 5.00, 8.00, 12.0, 12.0, 12.0, 14.0, 14.0, 17.0, and 20.0 m/s. find the particles’ average speed.
What is the root-mean-square speed of helium atoms in a balloon of diameter 30.0 cm at 20.00C and 1.00 atm?
Estimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapor and other constituents) in a room of capacity 25.0 m3 at a temperature of 270C and 1 atm pressure.
In a 30.0-s interval, 500 hailstones strike a glass window with an area of 0.600 m2 at an angle of 45.0° to the window surface. Each hailstone has a mass of 5.00 g and a speed of 8.00 m/s. If the collisions are elastic, what is the pressure on the window?
Four liters of a diatomic ideal gas ( λ =1.4) confined to a cylinder is subject to a closed cycle. Initially, the gas is at 1.00 atm and at 300 K. First, its pressure is tripled under constant volume. Then, it expands adiabatically to its original pressure. Finally, the gas is compressed isobarically to its original volume. Find the temperature at the end of the cycle
An oxygen cylinder of volume 30 litre has 18.20 moles of oxygen. After some oxygen is withdrawn from the cylinder, its gauge pressure drops to 11 atmospheric pressure at temperature 27°C. The mass of the oxygen withdrawn from the cylinder is nearly equal to:
[Given, R=100/12 J mol−1K−1, and molecular mass of O2=32, 1 atm pressure = 1.01×105 N/m2.
The molecule of a monatomic gas has only three translational degrees of freedom. Thus, the average energy of a molecule at temperature 'T' is __________.