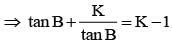UP PGT Math Mock Test - 1 - UPTET MCQ
30 Questions MCQ Test - UP PGT Math Mock Test - 1
Consider the following statements:
I: If A = {x: x is an even natural number} and B = {y: y is a natural number}, A subset B.
II: Number of subsets for the given set A = {5, 6, 7, 8) is 15.
III: Number of proper subsets for the given set A = {5, 6, 7, 8) is 15.
Which of the following statement(s) is/are correct?
If a,b,c are integers not all equal andw is a cube root of unity (ω ≠ 1) then the minimum value of |a + bω+ cω2| is
Let f be a real valued function defined on (0, 1) ∪ (2, 4) such that f ‘ (x) = 0 for every x, then
If the sum of the roots of the equation ax2 + bx + c = 0 is equal to sum of the squares of their reciprocals, then bc2 , ca2 , ab2 are in
If A, B, C are angles of a triangle ABC, then
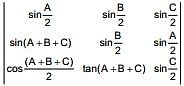
is less than or equal to
A coin is tossed n times. The probability of getting head at least once is greater than 0.8. Then the least value of n is
Let two numbers have arithmetic mean 9 and geometric mean 4. Then these numbers are the roots of the quadratic equation
Nidhi has 6 friends. In how many ways can she invite one or more of them to a party at her home?
Two matrices A and B are multiplicative inverse of each other only if
A fair die is tossed eight times. The probability that a third six is observed on the eight throw is
The coefficient of y in the expansion of (y² + c/y)5 is
If the roots of the cubic equation ax3 + bx2 + cx + d = 0 are in G.P., then
For any two non-zero complex numbers z1 and z2 if then the difference of amplitudes of z1 and z2 is
The equation of a circle which is concentric to the given circle x2 + y2 - 4x - 6y - 3 = 0 and which touches the Y-axis is:
If n (P) = 5, n(Q) = 12 and n(P U Q) = 14 then n(P ∩ Q) =
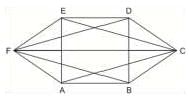
Three of the six vertices of a regular hexagon are chosen at random. The probability that the triangle with these vertices is equilateral is:
If n is a +ve integer, then the binomial coefficients equidistant from the beginning and the end in the expansion of (x+a)n are
A batsman scores runs in 10 innings 38,70,48,34,42,55,63,46,54 and 44, then the mean deviation is
Let R be the relation on N defined as x R y if x + 2 y = 8. The domain of R is
In a triangle ABC if A = π/4 and tanB tanC = K, then K must satisfy.



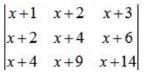
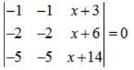
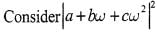
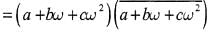
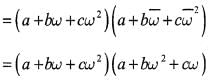
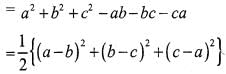
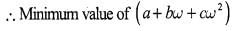

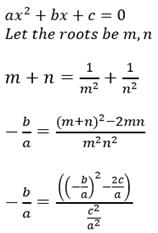

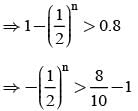


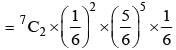
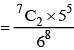
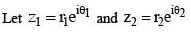
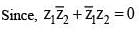
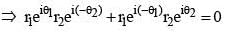
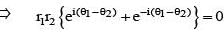
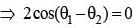
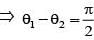
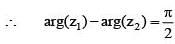
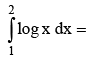

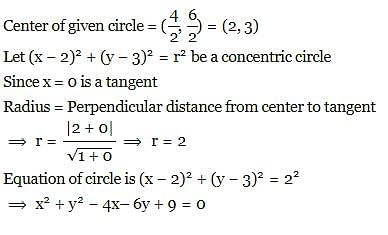
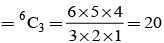
 is equal to
is equal to