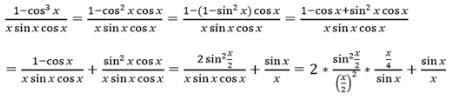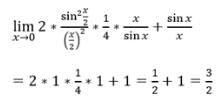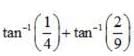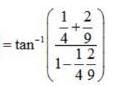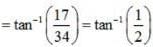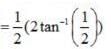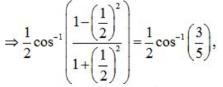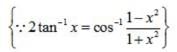UP PGT Math Mock Test - 5 - UPTET MCQ
30 Questions MCQ Test - UP PGT Math Mock Test - 5
Let A0 A1A2A3 A4A5 be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths of the line segments A0A1, A0 A2 and A0 A4 is
The y-intercept of the circle x2 + y2 + 4x + 8y - 5 = 0 is
The angle between line and plane 3x – 2y + 6z = 0 is (μ is scalar)
Let z(α,β) = cosα + eiβ sinα (α, β ∈ R, i = √-1) then the exhaustive set of values of modulus of z(θ, 2θ), as θ varies, is
Given n(U) = 20, n(A) = 12, n(B) = 9, n(A ∩ B) = 4, where U is the universal set, A and B are subsets of U, then n((A ∪ B)c) =
The tangent from the point of intersection of the lines 2x – 3y + 1 = 0 and 3x – 2y –1 = 0 to the circle x2 + y2 + 2x – 4y = 0 is
If P(n) is the statement; 4 + 8 + 12 +……+ 4n = 2n (n + 1) then P(6) will be
The exponent of power of x occurring in the 7th term of expansion of
Number of positive integral ordered pairs of (a, b) such that 6, a, b are in H.P is
The digits of a positive integer having three digits are in AP and sum of their digits is 21. The number obtained by reversing the digits is 396 less than the original number. Find the original number.
In case of strict decreasing functions, slope of tangent and hence derivative is
If a, b are the roots of x2 + px + q = 0, and w is a cube root of unity, then value of (ωα + ω2β)(ω2α + ωβ) is
The sum of the binomial coefficients of the 3rd, 4th terms from the beginning and from the end of (a + x)n is 440 then n =
The area bounded by the curve y = 4x - x2 and the x- axis is equal to
The number of triangles that can be formed with 6 points on a circle is
The function f : C → C defined by f (x)  for x ∈ C where bd ≠ 0 reduces to a constant function if
for x ∈ C where bd ≠ 0 reduces to a constant function if
Numbers greater than 1000 but not greater than 4000 are to be formed with the digits 0, 1, 2, 3, 4, allowing repetitions, the number of possible numbers is


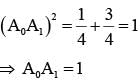
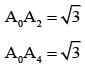
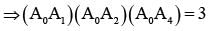
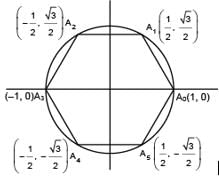

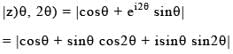
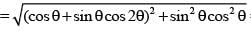
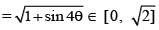
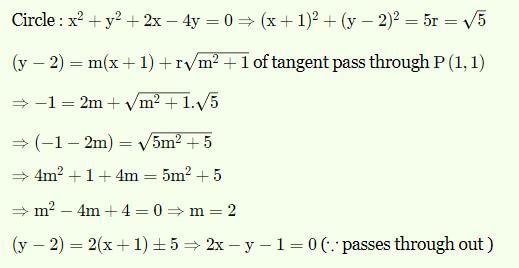
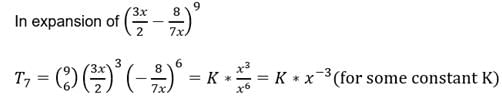
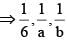 are in A.P.
are in A.P.
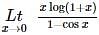 is equal to
is equal to