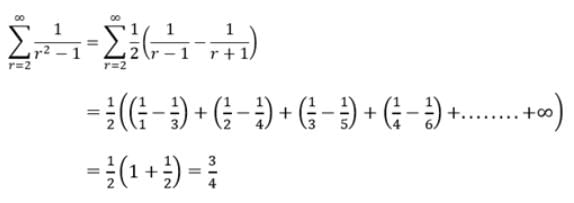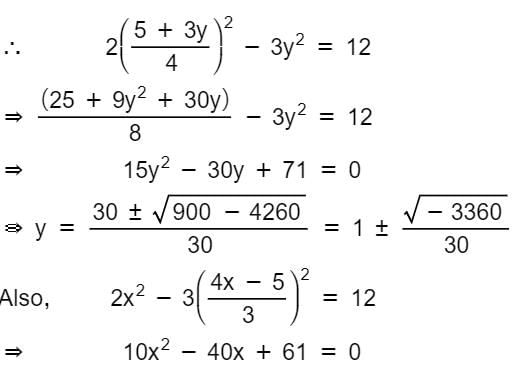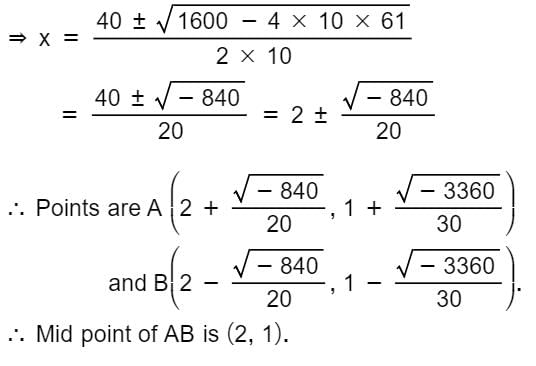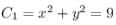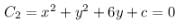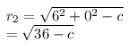UP PGT Math Mock Test - 9 - UPTET MCQ
30 Questions MCQ Test - UP PGT Math Mock Test - 9
A variable chord PQ of the parabola y = 4x2 substends a right angle at the vertex. Then the locus of points of intersection of the tangents at P and Q is
If ar > 0, r ∈ N and a1, a2 , a3 , .............a2n are A.P. then
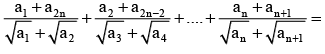
Find the result in the form a + ib of (2-√-25) / (1+√-16)
If a, b, c are in H.P., then the straight line always passes through a fixed point. That point is
Let a and b be non–zero real numbers. Then, the equation (ax2 + by2 + (C) (x2 – 5xy + 6y2) = 0 represents
The area enclosed by the parabola y2 = 2x and its tangents through the point (-2 , 0) is
If U = set of all whole numbers less than 12, A = set of all whole numbers less than 10, B = Set of all odd natural numbers less than 10, then what is (A ∩ B)’?
The point from which the tangents to the circles x2 + y2 – 8x + 40 = 0, 5x2 + 5y2 – 25 x + 80 = 0, x2 + y2 – 8x + 16y + 160 = 0 are equal in length is
If repetitions are not permitted
(i) How many 3 digit numbers can be formed from the six digits 2, 3, 5, 6, 7 & 9 ?
(ii) How many of these are less than 400 ?
(iii) How many are even ?
(iv) How many are odd ?
Let A {a, b, c} and let R = {(a, a)(a, b), (b, a)}. Then, R is
The equation to the common tangents to the two hyperbolas and
are
In the following case, determine whether the given planes are parallel orperpendicular, and in case they are neither, find the angles between them. 2x + y + 3z – 2 = 0 and x – 2y + 5 = 0
If f (x + y) = 2f (x) f (y) for all x, y ∈ R where f ' (0) = 3 and f (4) = 2, then f ' (4) is equal to
Find the equation of a curve passing through the point (0, –2) given that at any point (x, y) on the curve, the product of the slope of its tangent and y coordinate of the point is equal to the x coordinate of the point.
The mid-point of the chord 4x – 3y = 5 of the hyperbola 2x2 - 3y2 = 12 is
The sum of all 2-digited numbers which leave remainder 1 when divided by 3 is
If the circle x2 + y2 = 9 touches the circle x2 + y2 + 6y + c = 0, then c is equal to


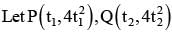
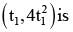
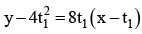
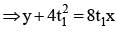
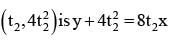
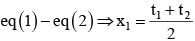
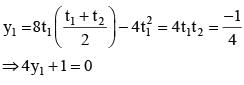
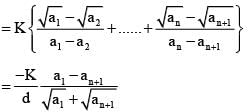


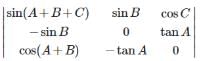
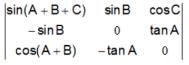
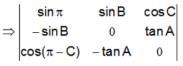
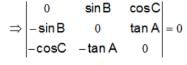
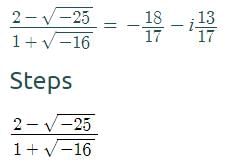
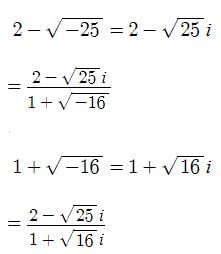
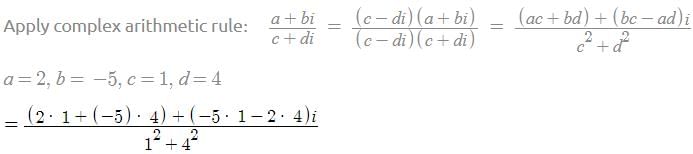
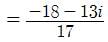
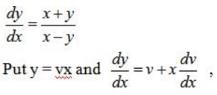
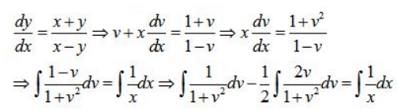
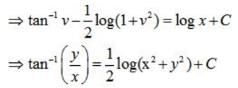
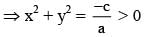

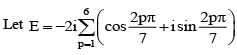
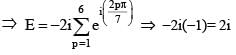
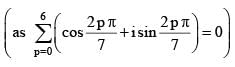
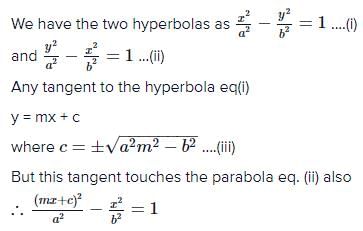
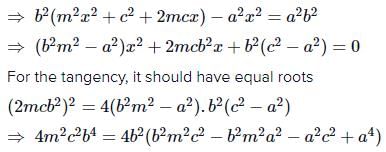
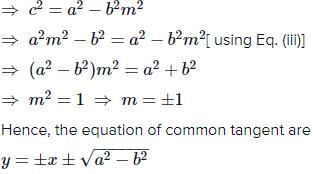
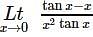 is equal to
is equal to