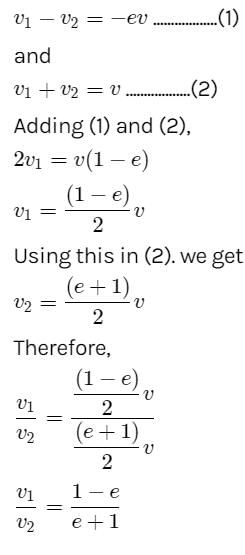Test: Collisions - NEET MCQ
10 Questions MCQ Test - Test: Collisions
A bomb of mass 4 kg explodes in air into two pieces of masses 3 kg and 1 kg. The smaller mass goes at a speed of 90 m/s. The total energy imparted to two fragments is.
In an elastic collision in one dimension if a body A collides against the body B of equal mass at rest, then the body A will
Which physical quantity is conserved during both elastic and inelastic collision?
A moving white hockey puck collides elastically with a stationary red hockey puck on a frictionless horizontal surface. No net external force acts on the two-puck system. Select all of the following statements that must be true for this elastic collision.
1. The kinetic energy of the white puck is conserved (same before and after the collision)
2. The linear momentum of the white puck is conserved.
3. The linear momentum of the two puck system is conserved.
A large mass M moving with velocity v makes an elastic head-on collision with a small mass m at rest. What will be the expression for energy lost by mass M?
A bomb at rest on a horizontal frictionless surface explodes and breaks into three pieces that fly apart horizontally as shown below. Select all of the following statements that must be true after the bomb has exploded.
1. The total kinetic energy of the bomb fragments is the same as that of the bomb before explosion.
2. The total momentum of the bomb fragments is the same as that of the bomb before explosion.
3. The total momentum of all the bomb fragments together is zero.
If a ball of mass 1 kg makes a head-on collision with a ball of an unknown mass initially at rest such that the ball rebounds to one third of its original speed, what is the mass of the other ball?
When a ball is allowed to fall from a height of 20 m, 40% of its energy is lost due to impact. After one impact the ball will go up to a height of
A particle of mass m moving with constant velocity v strikes another particle of same mass m but moving with the same velocity v in opposite direction stick together. The joint velocity after collision will be
There is a sphere of mass m moving with constant velocity v. It hits another sphere of same mass which is at rest. If e is the coefficient of restitution, then the ratio of the velocities of the two spheres after collision will be