Test: Counting Theorems
17 Questions MCQ Test | Test: Counting Theorems
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
n (P) = 5, n(Q) = 12 and n(PUQ) = 14
n(PUQ) = n(P) + n(Q) - n(P∩Q)
14 = 5 + 12 + - n(P∩Q)
n(P∩Q) = 3
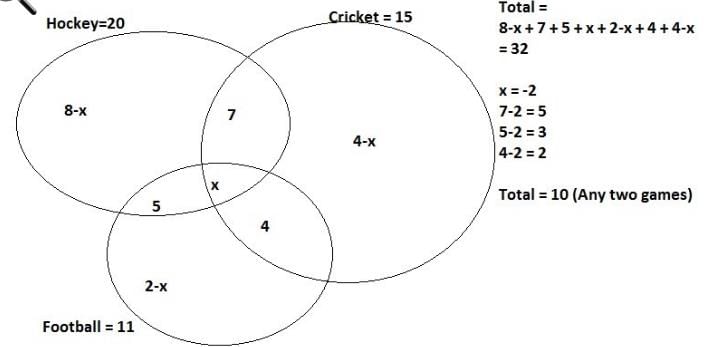
In a class of 50 students, 20 play Hockey, 15 play Cricket and 11 play Football. 7 play both Hockey and Cricket, 4 play Cricket and Football and 5 play Hockey and football. If 18 students do not play any of these given sports, how many students play exactly two of these sports?
Let A and B be two finite disjoint sets such that n(A ∪ B) = 475 and n(A) = 435, then n(B) is
As a and b are disjoint sets, they have no elements in common. Thus,
n(a∪b) = n(a) + n(b)
→n(b) = n(a∪b) − n(a)
= 475 − 435
= 40
If n(A) + n(B) + n(C) = n(A U B U C) then what are the sets A, B, C are called?
A and B are disjoint set so their is no common element between A and B.
n(AuBuC) = n(A)+n(B)+ n(C)-n(AnB)-n(Anc)-n(BnC)+n(AnBnC)
As we know n(AuB)=n(A)+ n(B)-n(AnB)
Here when we add A and B we are adding (AnB) two times , as it is present in both A and B. So we subtract (AnB) one time from A and B.
Which means we need to take the area of A and B set but no area should repeat.
When we take three sets A,B and C
We take area of A+ Area of B + area of C ————eq
But they are intersecting so the area we are taking is greater than actual area. We have again added (AnB), (AnC) and (BnC) twice. Therefore we subtract the intersecting area from eq one time as done above
A+B+C-(AnB)-(AnC)-(BnC)
The intersection of the sets a and b is the set of all the elements which belong to both A and B. It is denoted by A ∩ B (“A intersection B”).
• If A and B do not have any element in common then A ∩ B= a null set = Ø.
If in class XI of a certain school, 24 students got distinction in mathematics, 19 students got distinction in physics and 15 students got distinction in both the subjects, then the number of students in class XI is:
r :- c
Explanation:- Students got distinction in mathematics = 24
Student got distinction in physics = 19
Students got distinction in both= 15
Total number of students = (24+19)-15
= 28
There is a group of 80 persons who can drive scooter or car or both. Out of these, 35 can drive scooter and 60 can drive car. Find how many can drive both scooter and car? How many can drive scooter only? How many can drive car only?(Respectively)
Let S = {Persons who drive scooter}
C = {Persons who drive car}
Given, n(S ∪ C) = 80, n(S) = 35, n(C) = 60
Therefore, n(S ∪ C) = n(S) + n(C) - n(S ∩ C)
80 = 35 + 60 - n(S ∩ C)
80 = 95 - n(S ∩ C)
Therefore, n(S ∩ C) = 95 – 80 = 15
Therefore, 15 persons drive both
scooter and car.
Therefore, the number of persons who
drive a scooter only = n(S) - n(S ∩ C)
= 35 – 15
= 20
Also, the number of persons who drive car only = n(C) - n(S ∩ C)
= 60 - 15
= 45
If P and Q are two sets such that n(P) = 120, n(Q) = 50 and n(P ∪ Q) = 140 then, n(P ∩ Q) is:
If two sets A and B are having 99 elements in common, then the number of elements common to each of the sets A × B and B × A are
n((A × B) ∩ (B × A)) = n((A ∩ B) × (B ∩ A)) = n(A ∩ B).n(B ∩ A)
= n(A ∩ B).n(A ∩ B) = (99).(99) = 992.
If U = 100, n(A) = 30, n(B) = 40, n(A ∩ B) = 10, then n( A' ∩ B' ) =
By demorgan's law
n( A' ∩ B' )=n(A ∪ B)' = n(U) - n(A ∪ B)
=100 - [ n(A) + n(B) - n(A ∩ B) ]
=100 - 60 = 40
The number of non-empty subsets of the set {1, 2, 3, 4} is
The number of non- empty subsets =
2n − 1 = 24 − 1 = 16 − 1 = 15
A group of 120 students, 90 take mathematics and 72 take economics. If 10 students take neither of the two, how many students take both:
P(U) = 120
Mathematics = P(A) = 90
Economics = P(B) = 72
P(A ∪ B)' = 10
P(A ∪ B) = P(U) - P(A ∪ B)'
= 120 - 10 = 110
P(A ∪ B) = P(A) + P(B) - P(A ∪ B)
110 = 90 + 72 -P(A ∩ B)
P( A ∩ B) = 162 - 110 = 52
In a class of 50 students, 35 students play cricket and 30 students play football; identify the students playing both the games.
In a class of 40 students 14 take physics and 29 take chemistry. If 5 students take both, how many students take neither of the subjects?
Total students who took any of the subjects = 40 - x
Let x be the no. of students who took neither of the subjects
Then, 40 - x = 14 + 29 - 5
⇒ x = 2
N(A) indicates the number of elements in set A, there are 4 elements.
A={4,6,10} B={6,8}
A-B={4,10}
= n(A-B) = 2 Elements
A,B,C are three sets such that n(A) = 25, n(B) = 20, n(c) = 27, n(A ∩ B) = 5, n(B ∩ C ) = 7 and A ∩ C = ∅ then n(A ∪ B ∪ C) is equal to
Here A ∩ C = Ø ⇒ A ∩ B ∩ C = Ø
n (A ∪ B ∪ C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(B ∩ C) - n(C ∩ A) + n(A ∩ B ∩ C)
= 25 + 20 + 27 - 5 - 7 - 0 - 0
= 60
In a factory 70% of the workers like oranges and 64% like apples. If x% like both oranges and apples, then
let the total number of workers be 100. A = who likes oranges , B = who likes apples
So n(A ) = 70 and n(B) = 64, n(A ∩ B) = x
Also n(A U B) ≤ 100
n(A) + n(B) -n(A ∩ B) ≤ 100
70 + 64 - x ≤ 100
x ≥ 34
and n(A ∩ B) ≤ n(B) ⇒ x ≤ 64
then 34 ≤ x ≤ 64
Download free EduRev App
(Scan QR code)
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
