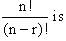Test: Permutations Non Distinct Objects - Commerce MCQ
20 Questions MCQ Test - Test: Permutations Non Distinct Objects
Sonia has 10 balloons out of which 5 are red, 2 white, 2 blue and 1pink, which she wants to use for the decoration. Her favourite pink colour balloon should be filled with toffees and should be put at the centre of the room above the cake table and remaining 9 at the wall behind the cake table. How many ways she can arrange the balloons?
In how many ways can 3 letters be posted in 4 letter boxes?
Among 7 flags 4 are of red colour and the rest are all different colours. How mant different signals can be generated using these flags?
If (n + 1)! = 20(n – 1)!, then n is equal to
There are 3 white, 4 red and 1 blue marbles in a bag. They are drawn one by one and arranged in a row. Assuming that all 8 marbles are drawn, determine the number of different arrangements if marbles of same colour are indistinguishable.
The number of permutations of n different objects taken r at a time, where repetition is allowed
In a class 6 students have to be arranged for a photograph. If the prefect and the vice must occupy the positions at either ends, how many ways the students can be arranged?
How many different words can be formed using the letters of the word BHARAT, which begin with B and end with T?
Find the number of words with or without meaning which can be made using all the letters of the word SWEET.
How many ways can three white and three red balloons be arranged in a row?
Out of 7 consonants and 4 vowels, how many words of 3 consonants and 2 vowels can be formed?
In a room there are 2 green chairs, 3 yellow chairs and 4 blue chairs. In how many ways can Raj choose 3 chairs so that at least one yellow chair is included?
In how many ways can 10 people line up at a ticket window of a cinema hall?
The number of permutation of n objects, where p1 objects are of one kind, p2 objects are of second kind, and so on till pk objects are of kth kind and rest, if any, are of different kinds is
In a group of 6 boys and 4 girls, four children are to be selected. In how many different ways can they be selected such that at least one boy should be there?
Number of signals that can be made using given 4 flags of which 3 are blue and 1 is red?
A coin is tossed 6 times, in how many throws can 4 heads and 2 tails be obtained?
How many three letter codes can be formed by only vowels of English alphabets, given that repetition of letters is allowed?