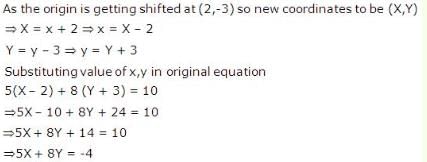Test: Shifting Of Origin - JEE MCQ
10 Questions MCQ Test - Test: Shifting Of Origin
What will be the new equation of the straight line 3x + 4y = 15, if the origin gets shifted to (1,-3) ?
What will be the new equation of the straight line 5x + 8y = 10, if the origin gets shifted to (2,-3) ?
The point where all the angle bisectors of a triangle meet is
What will be the new equation of the straight line 5x + 8y = 10, if the origin gets shifted to (2,-3) ?
What will be the value of ‘p” if the equation of the straight line 3x + 5y = 10 gets changed to 3x + 5y = p after shifting the origin at (2,2) ?
The distance between the pair of points (7,8) and (4,2) ,if origin is shifted to (1,-2) ,would be
The coordinates of centroid of triangle whose vertices are A(-1,-3), B(5,-6) and C(2,3) and origin gets shifted to (1,2)
New coordinates of the point (7,-1) would be, if the origin is shifted to the point (1,2) by translation of the axis.