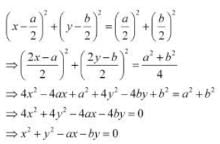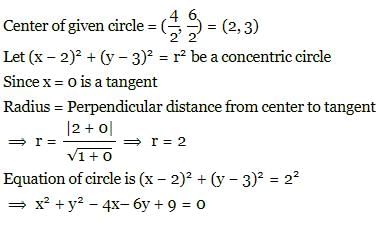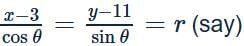Test: Circle- 1 - JEE MCQ
10 Questions MCQ Test - Test: Circle- 1
The equation of the circle passing through (0, 0) and making intercepts 2 and 4 on the coordinate axes is:
The equation of circle whose centre is (2, 1) and which passes through the point (3, – 5) is:
The equation of circle of radius 5 units touches the coordinates axes in the second quadrant is:
The equation of the circle passing through (0, 0) and making intercepts a and b on the coordinate axes is:
The equation of a circle which touches the straight lines x + y = 2, x − y = 2 and also touches the circle x2 + y2 = 1, is
The equation of a circle which is concentric to the given circle x2 + y2 - 4x - 6y - 3 = 0 and which touches the Y-axis is:
A line is drawn through the point P(3, 11) to cut the circle x2 + y2 = 9 at A and B. Then PA .PB is equal to
The intercept on the line y = x by the circle x2 + y2 − 2x = 0 is AB. Equation of the circle on AB as a diameter is