Test: Simple Harmonic Motion - NEET MCQ
10 Questions MCQ Test - Test: Simple Harmonic Motion
The velocity of a particle moving with simple harmonic motion is____ at the mean position.
A second pendulum is mounted in a space shuttle. Its period of oscillations will decrease when rocket is:
A particle of mass 10 gm lies in a potential field v = (50x2+100) J/kg. The value of frequency of oscillations in cycle/sec is
If a simple pendulum oscillates with an amplitude 50 mm and time period 2s, then its maximum velocity is:
In simple harmonic motion the displacement of a particle from its equilibrium position is given by 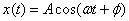 . Here the phase of motion is
. Here the phase of motion is
Find the amplitude of the S.H.M whose displacement y in cm is given by equation y= 3 sin157t + 4 cos157t, where t is time in seconds.
What will be the phase difference between bigger pendulum (with time period 5T/4 ) and smaller pendulum (with time period T) after one oscillation of bigger pendulum?
A particle executes linear simple harmonic motion with an amplitude of 2 cm. When the particle is at 1 cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then its time period in seconds is:



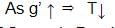

 ∴ We get, ω = √3 s-1
∴ We get, ω = √3 s-1










