Test: Illustrations of Bodies in Simple Harmonic Motion - Grade 12 MCQ
10 Questions MCQ Test - Test: Illustrations of Bodies in Simple Harmonic Motion
Two point masses of 3 Kg and 2 Kg are attached at the two ends of a horizontal spring with spring constant k=200N/m. Find the natural frequency of vibration of the system.
The instantaneous displacement of a simple harmonic oscillator is given by y = A cos (ωt + n/4). Its speed will be maximum at the time:). Its speed will be maximum at the time:
Due to what force a simple pendulum remains in simple harmonic motion?
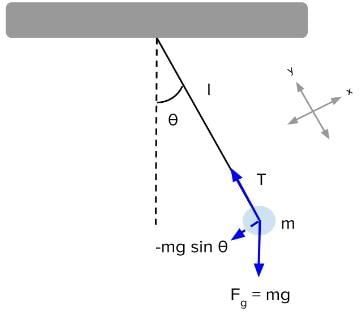
The motion of simple pendulum is said to be S.H.M when its angle θ¸ through which bob is displaced from its equilibrium position is
Two light springs of force constants k1 and k2, loaded with equal masses undergo vertical oscillations. If the maximum velocities of the masses are the same, the ratio of the amplitudes of oscillations is:
The work done by the string of a simple pendulum in S.H.M is
A simple pendulum with length l and bob of mass m is executing S.H.M of small amplitude a. The expression for maximum tension in the string will be
The amplitude A of a simple harmonic oscillator (with period, T and energy, E) is tripled. What would happen to T and E?
A simple pendulum is arranged using a small metallic bob of mass ‘m’and a light rubber cord of length ‘L’ (on suspending the bob), area of cross section ‘A’ and Young’s modulus ‘Y’. [One should use inextensible cord only for simple pendulum!]. When this unconventional pendulum is at rest in its mean position, the bob is pulled slightly down and is released. Then, the period of the vertical oscillation of the bob is (assuming that the size of the bob is negligible compared to the length of the cord):
A body of mass 5.0 kg is suspended by a spring which stretches 10 cm when the mass is attached. It is then displaced downward an additional 5.0 cm and released. Its position as a function of time is approximately: