Test: Center of Mass & its motion (14 July) - JEE MCQ
10 Questions MCQ Test - Test: Center of Mass & its motion (14 July)
When does the Center of Mass of a body lie outside the body itself?
In a system of multiple particles, how is the velocity of the Center of Mass determined?
Two particles A and B, initially at rest, move towards each other under the mutual force of attraction. At the instant when the speed of A is v and the speed of B is 2v, the speed of the centre of mass of the system is
Two small particles of equal masses start moving in opposite directions from a point A in a horizontal circular orbit. Their tangential velocities are v and 2v, respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at A, will these two particles again reach the point A?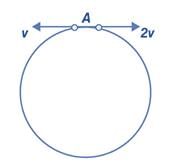
Two blocks of masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14 m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is
A 20g bullet pierces through a plate of mass M1=1kg and then comes to rest inside the second plate of mass M2 = 2.98 kg, as shown in the figure. It is found that the two plates initially at rest, now move with equal velocities. Find the percentage loss in the initial velocity of the bullet when it is between M1 and M2. Neglect any loss of material of the plates due to the action of a bullet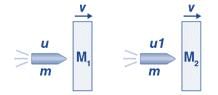
In a collinear collision, a particle with an initial speed V0 strikes a stationary particle of the same mass. If the final total kinetic energy is 50% greater than the original kinetic energy, the magnitude of the relative velocity between the two particles, after the collision, is
Two blocks A and B, each of mass m, are connected by a massless spring of natural length L and spring constant K. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in the figure. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B and collides elastically with A. Then