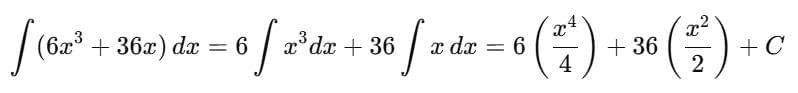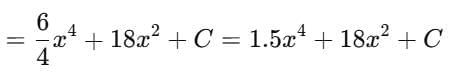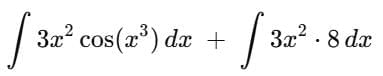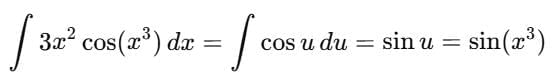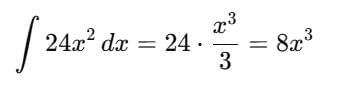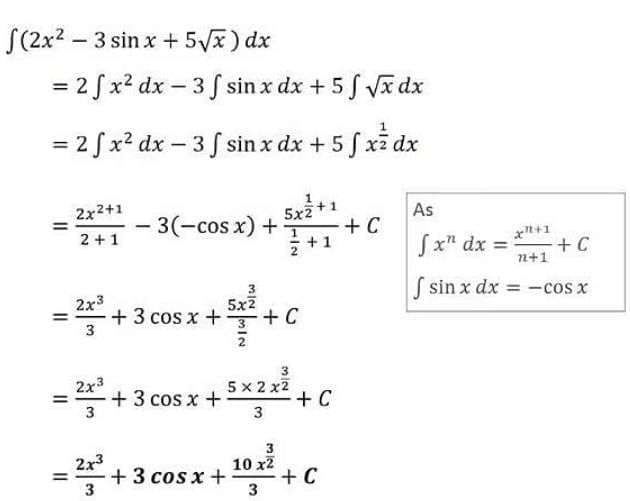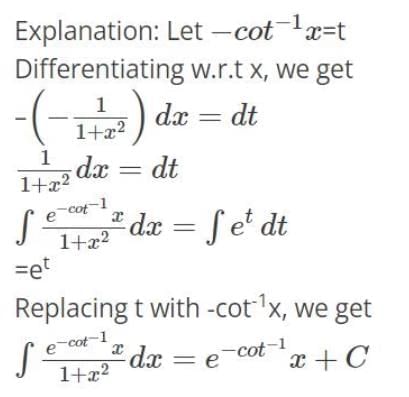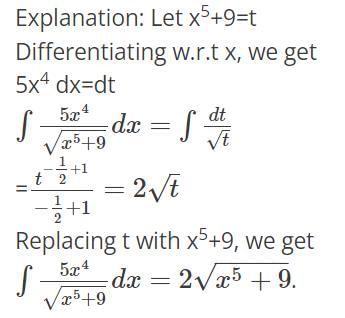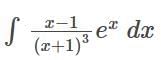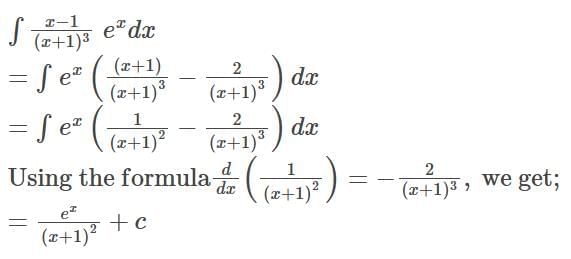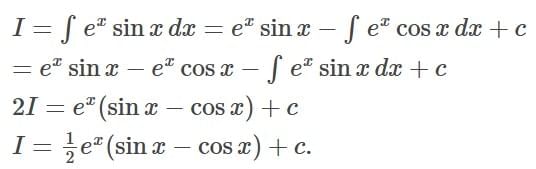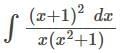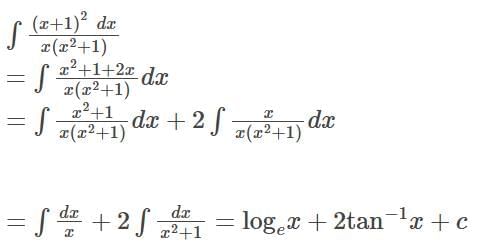Test: Integration Basics - JEE MCQ
Test Description
10 Questions MCQ Test - Test: Integration Basics
Test: Integration Basics for JEE 2025 is part of JEE preparation. The Test: Integration Basics questions and answers have been prepared
according to the JEE exam syllabus.The Test: Integration Basics MCQs are made for JEE 2025 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Integration Basics below.
Solutions of Test: Integration Basics questions in English are available as part of our course for JEE & Test: Integration Basics solutions in
Hindi for JEE course.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt Test: Integration Basics | 10 questions in 10 minutes | Mock test for JEE preparation | Free important questions MCQ to study for JEE Exam | Download free PDF with solutions
Detailed Solution for Test: Integration Basics - Question 1
Detailed Solution for Test: Integration Basics - Question 2
Detailed Solution for Test: Integration Basics - Question 3
Detailed Solution for Test: Integration Basics - Question 4
Detailed Solution for Test: Integration Basics - Question 5
Detailed Solution for Test: Integration Basics - Question 6
Detailed Solution for Test: Integration Basics - Question 7
Detailed Solution for Test: Integration Basics - Question 8
Detailed Solution for Test: Integration Basics - Question 9
Detailed Solution for Test: Integration Basics - Question 10
Information about Test: Integration Basics Page
In this test you can find the Exam questions for Test: Integration Basics solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Integration Basics, EduRev gives you an ample number of Online tests for practice
Download as PDF