Important Questions for Introduction To Vector Algebra
Find all the important questions for Introduction To Vector Algebra at EduRev.Get fully prepared for Introduction To Vector Algebra with EduRev's comprehensive question bank and test resources.
Our platform offers a diverse range of question papers covering various topics within the Introduction To Vector Algebra syllabus.
Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered.
The questions are designed to challenge you and help you gain confidence in tackling the actual exam.
Maximize your chances of success by utilizing EduRev's extensive collection of Introduction To Vector Algebra resources.
Introduction To Vector Algebra MCQs with Answers
Prepare for the Introduction To Vector Algebra within the JEE exam with comprehensive MCQs and answers at EduRev.
Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus.
Access the best books, study materials, and notes curated by toppers to enhance your preparation.
Stay updated with the exam date and receive expert preparation tips and paper analysis.
Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.
Online Tests for Introduction To Vector Algebra
Practice with a wide array of question papers that follow the exam pattern and syllabus.
Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement.
Access detailed solutions and explanations for each test to enhance your understanding of concepts.
With EduRev's Online Tests, you can build confidence, boost your performance, and ace Introduction To Vector Algebra with ease.
Join thousands of successful students who have benefited from our trusted online resources.



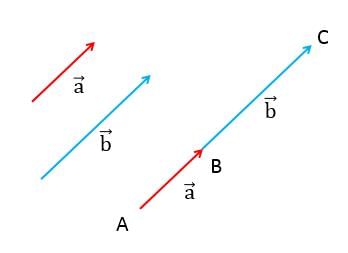
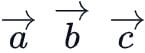 and
and 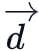 are the position vectors of the points A, B, C and D such that
are the position vectors of the points A, B, C and D such that 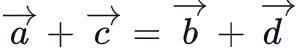 then ABCD is:
then ABCD is: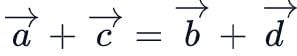

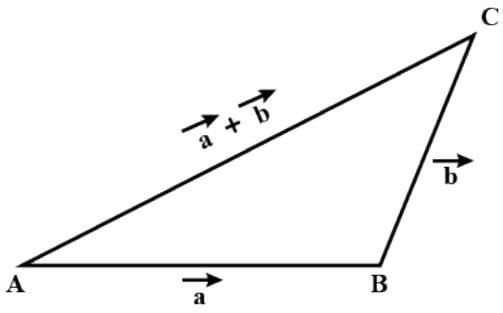
 then which of the following is true?
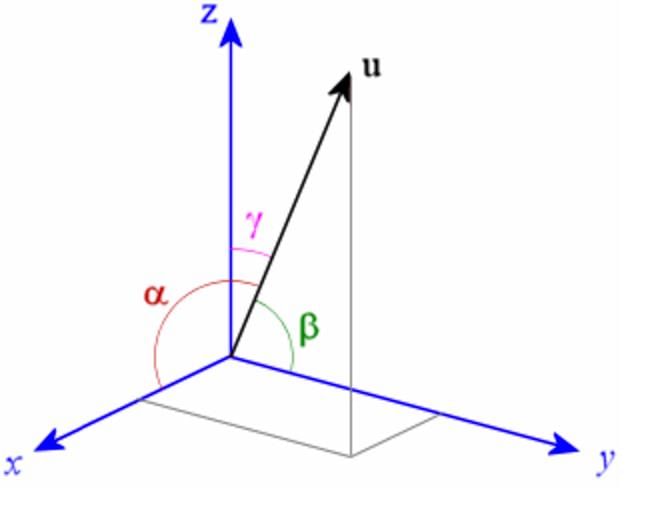
then which of the following is true?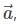 is the position vector of a point M(x,y,z) and α, β, γ are the angles, made by the vector
is the position vector of a point M(x,y,z) and α, β, γ are the angles, made by the vector 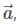 with the positive directions of x, y and z respectively. The cosines of the angles, cosα, cosβ, cosγ are the direction cosines of the vector
with the positive directions of x, y and z respectively. The cosines of the angles, cosα, cosβ, cosγ are the direction cosines of the vector 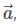 denoted by l, m, n, then
denoted by l, m, n, then










