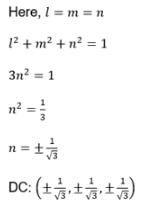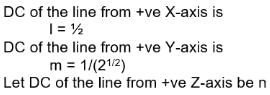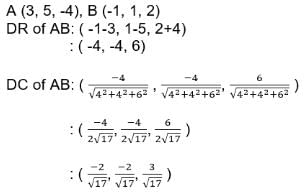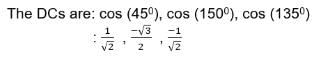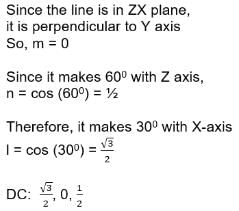All Courses
Get the App Signup / Login
Sign in Open App
JEE Exam  >  JEE Tests  >  Test: Introduction To 3D Geometry - JEE MCQ

Test: Introduction To 3D Geometry - JEE MCQ


Test Description

20 Questions MCQ Test - Test: Introduction To 3D Geometry

Test: Introduction To 3D Geometry for JEE 2024 is part of JEE preparation. The Test: Introduction To 3D Geometry questions and answers have been prepared according to the JEE exam syllabus.The Test: Introduction To 3D Geometry MCQs are made for JEE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Introduction To 3D Geometry below.
Solutions of Test: Introduction To 3D Geometry questions in English are available as part of our course for JEE & Test: Introduction To 3D Geometry solutions in Hindi for JEE course. Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt Test: Introduction To 3D Geometry | 20 questions in 20 minutes | Mock test for JEE preparation | Free important questions MCQ to study for JEE Exam | Download free PDF with solutions
Test: Introduction To 3D Geometry - Question 1
Save

Find the direction cosines of a line which makes equal angles with all three the coordinate axes.​

Detailed Solution for Test: Introduction To 3D Geometry - Question 1

Test: Introduction To 3D Geometry - Question 2
Save

Three planes, viz the XY Plane, XZ Plane and the YZ Plane divide the space into eight parts. Each part is called an OCTANT. What is the relation between these three planes​

Detailed Solution for Test: Introduction To 3D Geometry - Question 2

The three mutually perpendicular coordinate planes which in turn divide the space into eight parts and each part is known as octant.

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Introduction To 3D Geometry - Question 3
Save

The co-ordinates of the vertices of the triangle are A(-2, 3, 6), B(-4, 4, 9) and C(0, 5, 8). The direction cosines of the median BE are:​

Detailed Solution for Test: Introduction To 3D Geometry - Question 3


Test: Introduction To 3D Geometry - Question 4
Save

If the direction cosines of a line from the positive X-axis and Y-axis areThe angle of the line through Z-axis is:​
Detailed Solution for Test: Introduction To 3D Geometry - Question 4



Test: Introduction To 3D Geometry - Question 5
Save

The direction cosines of the line equally inclined with the axes are:​
Detailed Solution for Test: Introduction To 3D Geometry - Question 5

Test: Introduction To 3D Geometry - Question 6
Save

The direction cosines of the line whose direction ratios are 6, – 6, 3 are:
Detailed Solution for Test: Introduction To 3D Geometry - Question 6

Test: Introduction To 3D Geometry - Question 7
Save

Find the direction cosines of the x axis.​
Detailed Solution for Test: Introduction To 3D Geometry - Question 7

To find Direction Cosines of X-axis.
Take any two points on X-axis : A(a,0,0) & B(b,0,0)
DR of AB : (b-a,0,0)
DC of AB : ((b-a)/(((b-a)2 + 0 + 0)1/2), 0, 0)
: ((b-a)/(b-a) , 0 , 0)
: (1,0,0)

Test: Introduction To 3D Geometry - Question 8
Save

The direction cosines of the line joining the points (2, -1, 8) and (-4, -3, 5) are:
Detailed Solution for Test: Introduction To 3D Geometry - Question 8

Pt. A(2, -1, 8)
Pt. B(-4, -3, 5)
Direction Ratio DR of AB : ( -4-2 , -3+1 , 5-8 )
: (-6,-2,-3)
Direction cosine of AB : ( -6/(62+22+32)1/2 , -2/(62+22+32)1/2 , -3/(62+22+32)1/2)
: ( -6/7, -2/7, -3/7)
 

Test: Introduction To 3D Geometry - Question 9
Save

What are direction numbers of a line.​
Detailed Solution for Test: Introduction To 3D Geometry - Question 9

The numbers which are proportional to direction cosines of a line are called direction numbers of the line.

Test: Introduction To 3D Geometry - Question 10
Save

What are direction ratios of a line.​
Test: Introduction To 3D Geometry - Question 11
Save

Find the direction cosines of the side AB of the triangle whose vertices are A(3, 5, -4), B(-1, 1, 2) and C(-5, -5, -2)
Detailed Solution for Test: Introduction To 3D Geometry - Question 11

Test: Introduction To 3D Geometry - Question 12
Save

If l, m , n are the direction cosines of any line, then sum of the squares of the direction cosines of the line is always​
Test: Introduction To 3D Geometry - Question 13
Save

If a line has the direction ratios -4, 18, -12 then what are its direction cosines?​
Detailed Solution for Test: Introduction To 3D Geometry - Question 13

DR of the line :  (-4, 18 -12)
DC of the line : (-4/k, 18/k, -12/k)
where k = ((42) + (182) + (12)2)1/2
= (16 + 324 + 144)1/2
= (484)1/2
= 22
So, DC : (-4/22, 18/22, -12/22)
: (-2/11 , 9/11 , -6/11)

Test: Introduction To 3D Geometry - Question 14
Save

The direction cosines of the line equally inclined with the axes, are:​
Detailed Solution for Test: Introduction To 3D Geometry - Question 14
Cos^2 alpha+cos ^2 beta +cos^ 2 gamma =1
put alpha =beta. =gamma
we get cosalpha= 1/√3
DC's of given line (1/√3,1/√3,1/3)
Test: Introduction To 3D Geometry - Question 15
Save

If a line makes angles 45°,150°, 135°, with x, y and z-axes respectively, find its direction cosines.
Detailed Solution for Test: Introduction To 3D Geometry - Question 15

Test: Introduction To 3D Geometry - Question 16
Save

Find the equation of the set of points which are equidistant from the points (1, 2 , 3) and (3, 2, -1)​
Detailed Solution for Test: Introduction To 3D Geometry - Question 16

Pt. A(1, 2 , 3)
Pt. B(3, 2, -1)
Let P(x,y,z)
So, AP = BP
((x-1)2 + (y-2)2 + (z-3)2)1/2 = ((x-3)2 + (y-2)2 + (z+1)2)1/2
(x-1)2 + (y-2)2 + (z-3)2) = (x-3)2 + (y-2)2 + (z+1)2
x2 +1 -2x + y2 + 4 - 4y + z2 + 9 – 6z = x2 +9 -6x + y2 + 4 - 4y + z2 + 1 + 2z
4x – 8z = 0
x – 2z = 0

Test: Introduction To 3D Geometry - Question 17
Save

If a line in the ZX-plane makes an angle 60o with Z-axis, the direction cosines of this line are:
Detailed Solution for Test: Introduction To 3D Geometry - Question 17

Test: Introduction To 3D Geometry - Question 18
Save

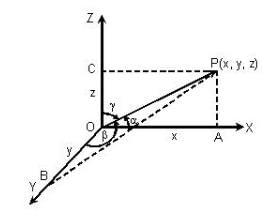
A line makes angles α, β, γ with the positive directions of X-axis, Y-axis and Z-axis, respectively, then the directions cosines of the line are:
Detailed Solution for Test: Introduction To 3D Geometry - Question 18

cos α, cos β, cos γ
By the definition of Direction Cosines

Test: Introduction To 3D Geometry - Question 19
Save

The signs of the X,Y and Z coordinates of a point that lies in the octant OXYZ’ is​
Detailed Solution for Test: Introduction To 3D Geometry - Question 19

X,Y,Z imply positive X,Y,Z axis & X’,Y’,Z’ imply negative X,Y,Z axis.
So, OXYZ’ will have a point of signs (+, +, -).

Test: Introduction To 3D Geometry - Question 20
Save

If a line in the ZX-plane makes an angle 30o with Z-axis, the direction cosines of this line are:
Detailed Solution for Test: Introduction To 3D Geometry - Question 20
The line makes 30o with z-axis

Since it is in z-x axis the angle made with y-axis is 90

And angle made by x-axis is 60

Therefore direction cosines are

1/2, 0, √3/2
Information about Test: Introduction To 3D Geometry Page
In this test you can find the Exam questions for Test: Introduction To 3D Geometry solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Introduction To 3D Geometry, EduRev gives you an ample number of Online tests for practice

Top Courses for JEE

Download as PDF

Top Courses for JEE

Important Questions for Introduction To 3D Geometry

Find all the important questions for Introduction To 3D Geometry at EduRev.Get fully prepared for Introduction To 3D Geometry with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Introduction To 3D Geometry syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Introduction To 3D Geometry resources.

Introduction To 3D Geometry MCQs with Answers

Prepare for the Introduction To 3D Geometry within the JEE exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Introduction To 3D Geometry

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Introduction To 3D Geometry with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup