CSIR NET Mathematics Mock Test - 1 - CSIR NET Mathematics MCQ
30 Questions MCQ Test - CSIR NET Mathematics Mock Test - 1
The average of four consecutive odd numbers is 30. What will be the value of the smallest number?
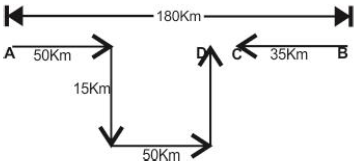
Two cars start from the opposite places of a main road which are at a distance of 180 km.. First car runs for 50 km and takes a right turn and then runs 15 km. It then turns left and then runs for another 50 km and then takes a left turn which takes it back to reach the main road. In the meantime, due to minor breakdown the other car has run only 35 km along the main road. What would be the distance between two cars at this point?
Rohan travels 13 km towards west from a point and then he turns left and travels 4 km. Again he turns by 135∘ clockwise direction and moves straight. In which direction is he facing now?
Ajit has a certain average for 9 innings. In the tenth innings, he scores 100 runs thereby increasing his average by 8 runs. His new average is:
Direction: In each of the following questions, a series is given with one/two term(s) missing. Choose the correct alternatives from the given ones that will complete the series.
10, 16.5, 36, 96, ?, 1074
Direction: In each of the following questions, a series is given with one/two term(s) missing. Choose the correct alternatives from the given ones that will complete the series.
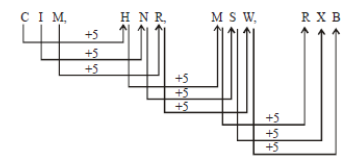
CIM, HNR, MSW, ?
Direction: In each of the following questions, a series is given with one/two term(s) missing. Choose the correct alternatives from the given ones that will complete the series.
BAB, CEC, DID, EOE, ?
By what least number should 128 be multiplied so that it becomes a perfect square?
An animal feed company must produce 200 kg of a mixture consisting of ingredients X1 and X2. The ingredient X1 costs Rs. 3 per kg and X2 costs Rs. 5 per kg. Not more than 80 kg of X1 can be used and at least 60 kg of X2 must be used.
Number of values of m ∈ N for which y = emx is a solution of the differential equation D3y - 3D2y - 4Dy + 12y = 0, where D is derivative:
If A = { x : x ∈ N, 0 < x < 6} and B = {x : x is a prime natural number, 0 < x < 10}. Find A - B.
The number of elements in the set are relatively primet is
are relatively primet is
An ice cream shop sells ice cream in five possible flavours: Vanilla, Chocolate, Strawberry, Mango and Pineapple. How many combinations of three scoop cones are possible? [Note: The repetition of flavours is allowed but the order in which the flavours are chosen does not matter]
Let A = [aij] be a matrix : aij = k ≠ 0, for every i,j, then rank (A) is -
The derivative of the function f(x) = sin n xis—
A function f(x) is defined as follows:

Then f(x) is:
For given 4(x, y) = x3 - 3xy2 + 3x2 - 3y2 + 1. The analytic function f(x) is
Given the function:
(A) Differentiable at x = 0
(B) f′ (0–) = 0
(C) f′ (0 + ) = 0
(D) f′(0 – ) ≠ f′ (0 + )

Given the function f(x) = |x
(A) Differentiable at x = 0
(B) Not differentiable at x = 0
(C) f′ (0 + ) = f′ (0 – )
(D) f′ (0 +) ≠ f′ (0 – )
Let p be a real polynomial of the real variable x of the form p(x) = xn + an – 1 xn –1 + … + a1x – 1. Suppose that p has no roots in the open unit disc and p(–1) = 0 Then—
The function f : R → R is given by f (x) = e|x + x2 + |x2 – 1| Which of the following is true about the function f ?
Consider the sequence of rational numbers {qk} k ≥ 1 where 











 gives the general solution -
gives the general solution -



 Dy
Dy 
 is:
is:




 (two values)
(two values) is
is



 and
and  .
.


 is a prime natural number,
is a prime natural number, 


 is a prime natural number,
is a prime natural number, 



 The value
The value  is
is  .
.


 AII Flavours are same
AII Flavours are same
 Two Flawomrs are same and one is different
Two Flawomrs are same and one is different

 is—
is—



 is
is The second term
The second term 

 th term
th term 



























