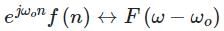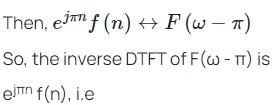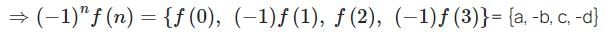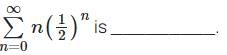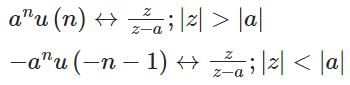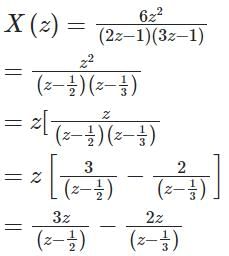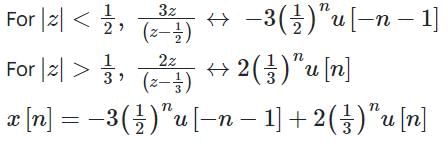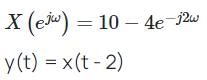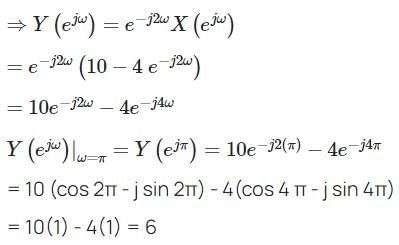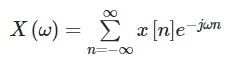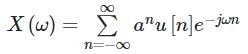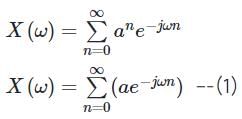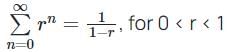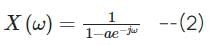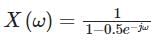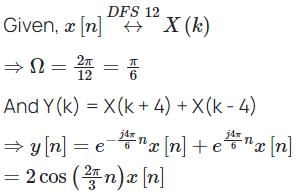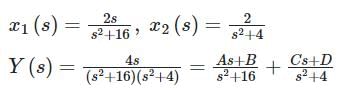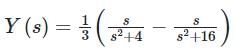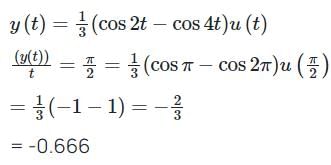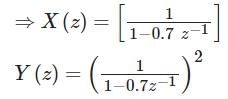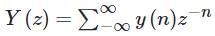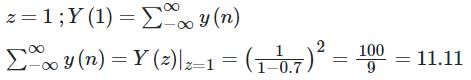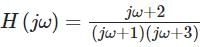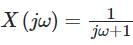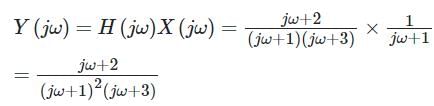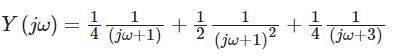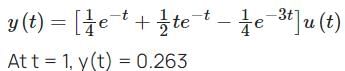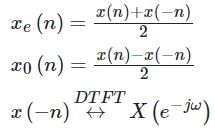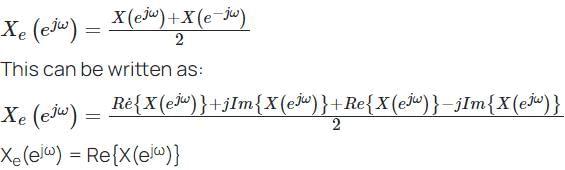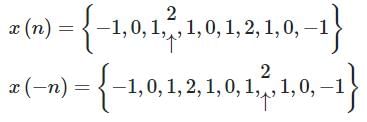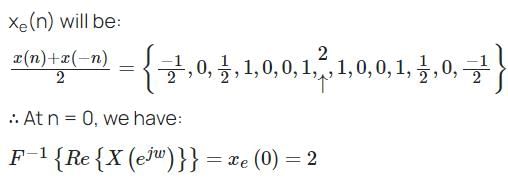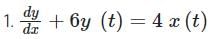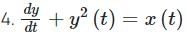Test: Signals & Systems - 2 - Electronics and Communication Engineering (ECE) MCQ
20 Questions MCQ Test - Test: Signals & Systems - 2
For a given periodic sequence x (n) = {1, 1, 0, 0} with period N = 4, the Fourier coefficient is denoted by ck. The Value of c3* is:
Consider the following difference equation:
y[n] + 3y[n – 1] + 2y[n – 2] = 2x[n] – x[n – 1]
If y[-1] = 0, y[-2] = 1, x[n] = u[n], then y[n] can be represented as
The Fourier series coefficients of a periodic signal x(t), with fundamental frequency 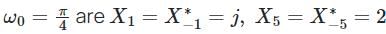 and the rest are zero. Suppose x(t) is the input to a band-pass filter with the following magnitude and phase responses.
and the rest are zero. Suppose x(t) is the input to a band-pass filter with the following magnitude and phase responses.
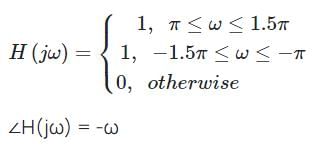
Let y(t) be the output of the filter and the Fourier series of x(t) in the trigonometric form
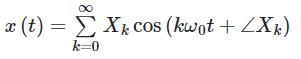
x(t) and the steady state response of y(t) are
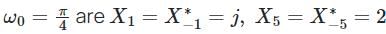 and the rest are zero. Suppose x(t) is the input to a band-pass filter with the following magnitude and phase responses.
and the rest are zero. Suppose x(t) is the input to a band-pass filter with the following magnitude and phase responses.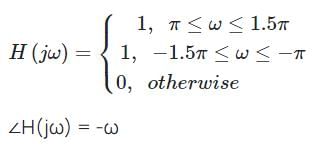
Let y(t) be the output of the filter and the Fourier series of x(t) in the trigonometric form
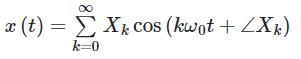
x(t) and the steady state response of y(t) are
The discrete Fourier series representation for the following sequence:
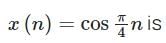
For a finite support signal x[n] = r[n] (u[n] – u[n – 11]) where r[n] is the discrete-time ramp function, the energy of x[n] is
The percentage of the total energy dissipated by a 1Ω resistor in the frequency band 0 < ω < 10 rad/s when the voltage across it is v(t) = e-2t u(t) is _________
The z-transform of a sequence x[n] is given as x(z) = 3 + 4z – 6z-1 + 2z-2
If y[n] is the first difference of x[n], then y(z) is given by
The DTFT of a signal f(n) = {a, b, c, d} is F(ω). The inverse DTFT of F(ω - π) is:
What is the signal corresponding to the following z-transform? (Where u[n] is the unit-step signal)
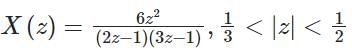
Let 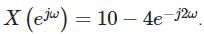 If y(t) = x(t - 2) then what is value of Y(ejω) at ω = π is ________
If y(t) = x(t - 2) then what is value of Y(ejω) at ω = π is ________
The DTFT of x[n] = 0.5n u[n] using geometric series is:
A discrete time signal x[n] and its discrete Fourier transform X(k) related by 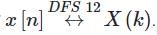 Another discrete series with Fourier coefficients Y(k) given as Y(k) = X(k - 4) + X(k + 4) then the corresponding sequence y[n] will be
Another discrete series with Fourier coefficients Y(k) given as Y(k) = X(k - 4) + X(k + 4) then the corresponding sequence y[n] will be
Consider a signal y(t) = x1(t) * x2(t). If x1(t) = 2 cos 4t u(t) and x2(t) = sin 2t u(t). The value of y(t) at t = π / 2 is _______
The sequence x[n] is (0.7)n u(n) and y (n) is x (n)*x (n). Then which of the following statement(s) is/are true?
Consider a system with frequency response of 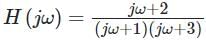 and suppose that the input to the system is x(t) = e-t u(t). If the output response is y(t), the value of y(1) is _______ (answer up to two decimal places)
and suppose that the input to the system is x(t) = e-t u(t). If the output response is y(t), the value of y(1) is _______ (answer up to two decimal places)
Let 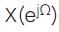 denote the Fourier transform of the signal x[n], where:
denote the Fourier transform of the signal x[n], where:
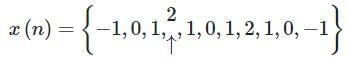
The value of 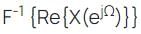 at n = 0 will be ________. (The arrow represents the origin)
at n = 0 will be ________. (The arrow represents the origin)
Which of the following systems are linear time-invariant and causal systems.


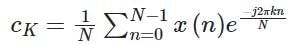
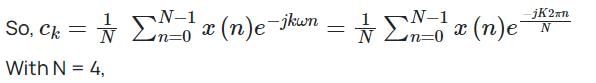
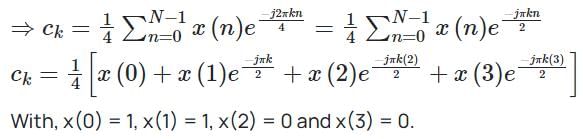
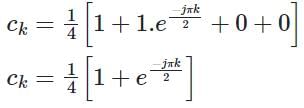
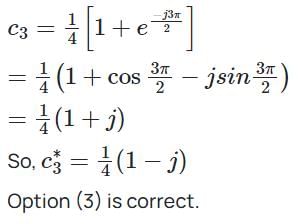
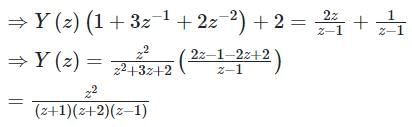
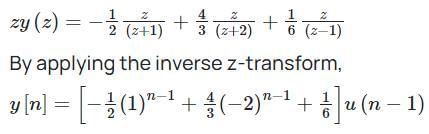

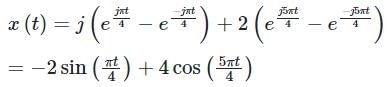
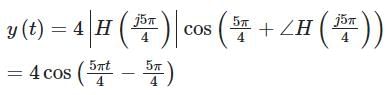
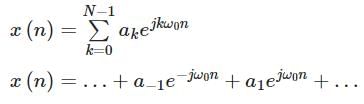
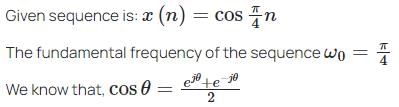
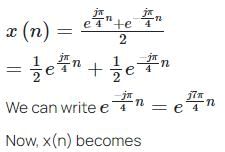
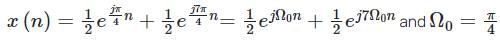
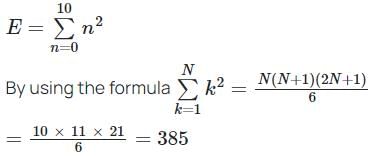
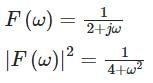

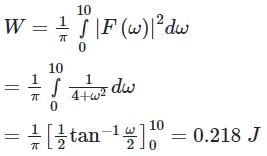

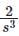 with ROC: Re (s) > 0.
with ROC: Re (s) > 0.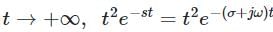 tends to zero for σ = Re(s) > 0 as the exponent term dominates and its integral from 0 to +∞ converges.
tends to zero for σ = Re(s) > 0 as the exponent term dominates and its integral from 0 to +∞ converges.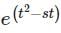 does not tend to zero as t → +∞, which means the integral from 0 to +∞ is unbounded for all s. Thus the Laplace transform cannot converge for any value of s.
does not tend to zero as t → +∞, which means the integral from 0 to +∞ is unbounded for all s. Thus the Laplace transform cannot converge for any value of s. does not tend to zero for t → -∞.
does not tend to zero for t → -∞.