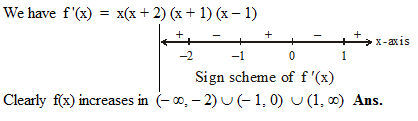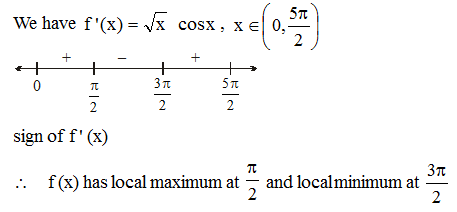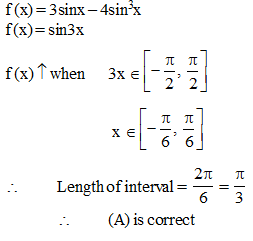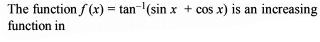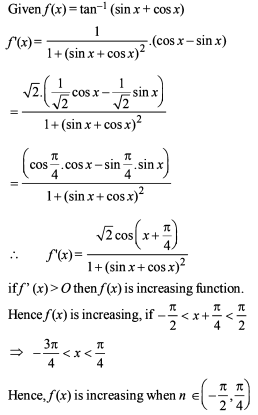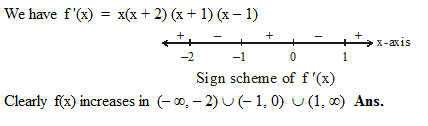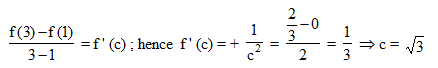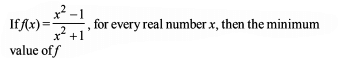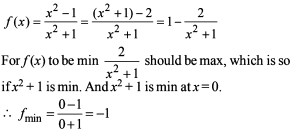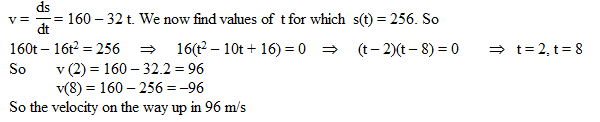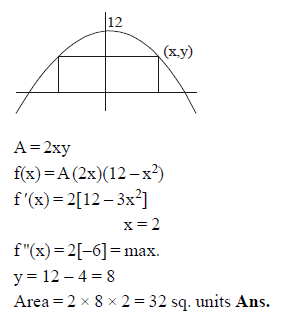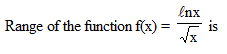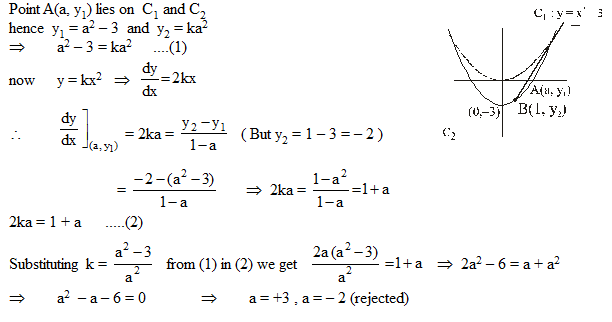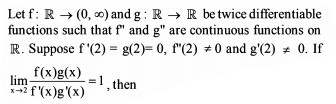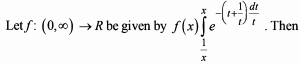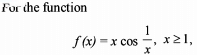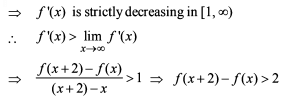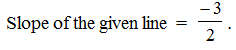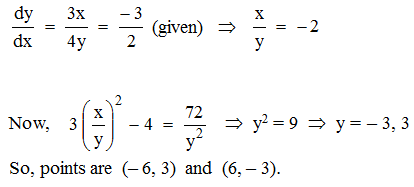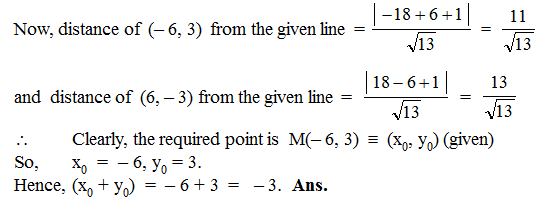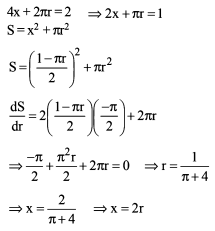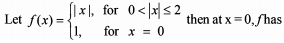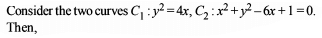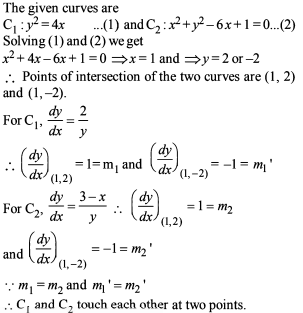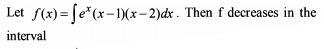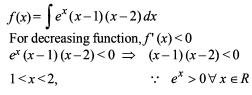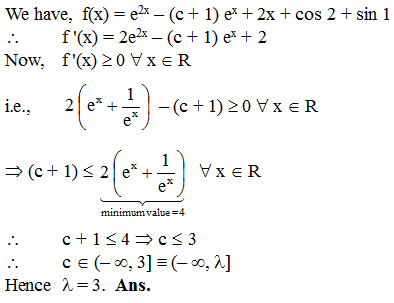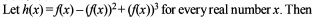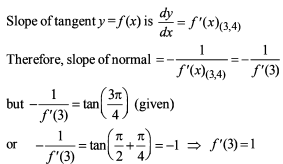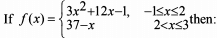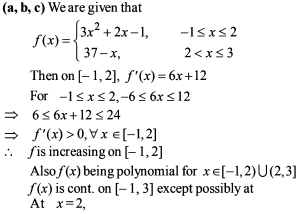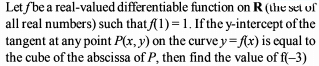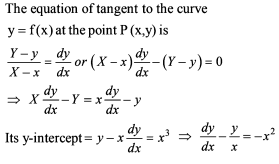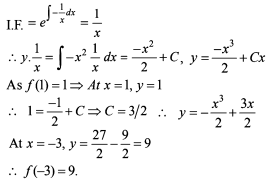Test: Application of Integrals - 3 - JEE MCQ
Test Description
30 Questions MCQ Test - Test: Application of Integrals - 3
Test: Application of Integrals - 3 for JEE 2025 is part of JEE preparation. The Test: Application of Integrals - 3 questions and answers have been prepared
according to the JEE exam syllabus.The Test: Application of Integrals - 3 MCQs are made for JEE 2025 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Application of Integrals - 3 below.
Solutions of Test: Application of Integrals - 3 questions in English are available as part of our course for JEE & Test: Application of Integrals - 3 solutions in
Hindi for JEE course.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt Test: Application of Integrals - 3 | 30 questions in 60 minutes | Mock test for JEE preparation | Free important questions MCQ to study for JEE Exam | Download free PDF with solutions
Test: Application of Integrals - 3 - Question 1
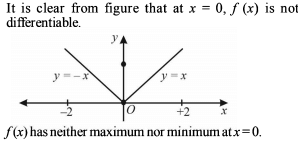
For which one of the following function Rolle's theorem is applicable?
Detailed Solution for Test: Application of Integrals - 3 - Question 1
Detailed Solution for Test: Application of Integrals - 3 - Question 2
Detailed Solution for Test: Application of Integrals - 3 - Question 3
Detailed Solution for Test: Application of Integrals - 3 - Question 4
Test: Application of Integrals - 3 - Question 5
The length of a longest interval in which the function f (x) = 3 sinx – 4 sin3x is increasing, is
Detailed Solution for Test: Application of Integrals - 3 - Question 5
Detailed Solution for Test: Application of Integrals - 3 - Question 6
Detailed Solution for Test: Application of Integrals - 3 - Question 7
Detailed Solution for Test: Application of Integrals - 3 - Question 8
Test: Application of Integrals - 3 - Question 9
A dynamite blast blows a heavy rock straight up with a launch velocity of 160 m/sec. It reaches a height of s = 160 t = 16t2 after t sec. The velocity of the rock when it is 256 m above the ground on the way up is
Detailed Solution for Test: Application of Integrals - 3 - Question 9
Test: Application of Integrals - 3 - Question 10
Find the area (in sq. units) of the largest rectangle with lower base on the x-axis & upper vertices on thecurve y = 12 – x2.
Detailed Solution for Test: Application of Integrals - 3 - Question 10
Detailed Solution for Test: Application of Integrals - 3 - Question 11
Test: Application of Integrals - 3 - Question 12
If the point P(a, b) lies on the curve 9y2 = x3 such that the normal to the curve at P makes equal intercepts with the axes. The value of
(a + 3b) is
Detailed Solution for Test: Application of Integrals - 3 - Question 12
Test: Application of Integrals - 3 - Question 13
Two curves C1 : y = x2 – 3 and C2 : y = kx2 , intersect each other at two different points. The tangent drawn to C2 at one of the points of intersection A (a,y1) , (a > 0) meets C1 again at B(1,y2) . The value of ‘a’ is
Detailed Solution for Test: Application of Integrals - 3 - Question 13
*Multiple options can be correct
Detailed Solution for Test: Application of Integrals - 3 - Question 14
*Multiple options can be correct
Detailed Solution for Test: Application of Integrals - 3 - Question 15
*Multiple options can be correct
Detailed Solution for Test: Application of Integrals - 3 - Question 16
Detailed Solution for Test: Application of Integrals - 3 - Question 17
Detailed Solution for Test: Application of Integrals - 3 - Question 18
Test: Application of Integrals - 3 - Question 19
If M (x0, y0) is the point on the curve 3x2 – 4y2 = 72, which is nearest to the line 3x + 2y + 1 = 0, then the value of (x0 + y0) is equal to
Detailed Solution for Test: Application of Integrals - 3 - Question 19
Detailed Solution for Test: Application of Integrals - 3 - Question 20
Detailed Solution for Test: Application of Integrals - 3 - Question 21
Detailed Solution for Test: Application of Integrals - 3 - Question 22
Detailed Solution for Test: Application of Integrals - 3 - Question 23
Detailed Solution for Test: Application of Integrals - 3 - Question 24
Test: Application of Integrals - 3 - Question 25
If the exhaustive set of all possible values of c such that f(x) = e2x – (c + 1) ex + 2x + cos 2 + sin 1, is monotonically increasing for all x ∈ R, is (–∞, λ], then find the value of λ.
Detailed Solution for Test: Application of Integrals - 3 - Question 25
*Multiple options can be correct
Detailed Solution for Test: Application of Integrals - 3 - Question 26
Detailed Solution for Test: Application of Integrals - 3 - Question 27
*Multiple options can be correct
Detailed Solution for Test: Application of Integrals - 3 - Question 28
Detailed Solution for Test: Application of Integrals - 3 - Question 29
Detailed Solution for Test: Application of Integrals - 3 - Question 30
Information about Test: Application of Integrals - 3 Page
In this test you can find the Exam questions for Test: Application of Integrals - 3 solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Application of Integrals - 3, EduRev gives you an ample number of Online tests for practice
Download as PDF
Important Questions for Application of Integrals - 3
Find all the important questions for Application of Integrals - 3 at EduRev.Get fully prepared for Application of Integrals - 3 with EduRev's comprehensive question bank and test resources.
Our platform offers a diverse range of question papers covering various topics within the Application of Integrals - 3 syllabus.
Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered.
The questions are designed to challenge you and help you gain confidence in tackling the actual exam.
Maximize your chances of success by utilizing EduRev's extensive collection of Application of Integrals - 3 resources.
Application of Integrals - 3 MCQs with Answers
Prepare for the Application of Integrals - 3 within the JEE exam with comprehensive MCQs and answers at EduRev.
Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus.
Access the best books, study materials, and notes curated by toppers to enhance your preparation.
Stay updated with the exam date and receive expert preparation tips and paper analysis.
Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.
Online Tests for Application of Integrals - 3
Practice with a wide array of question papers that follow the exam pattern and syllabus.
Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement.
Access detailed solutions and explanations for each test to enhance your understanding of concepts.
With EduRev's Online Tests, you can build confidence, boost your performance, and ace Application of Integrals - 3 with ease.
Join thousands of successful students who have benefited from our trusted online resources.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily