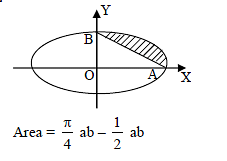
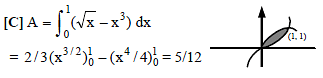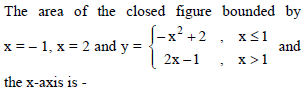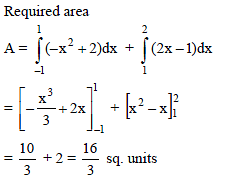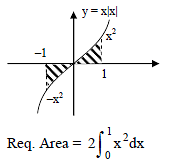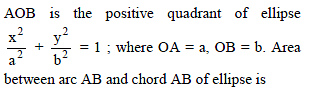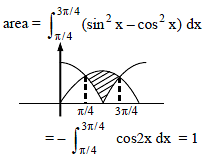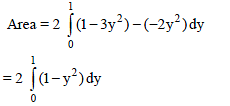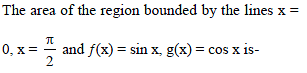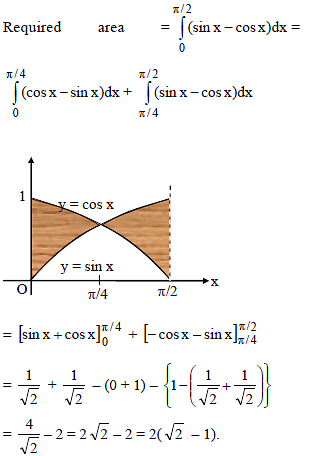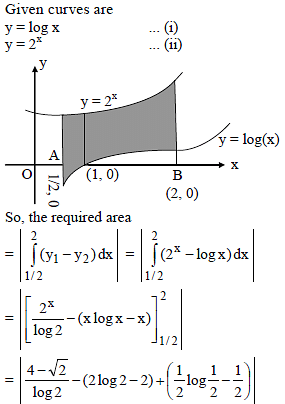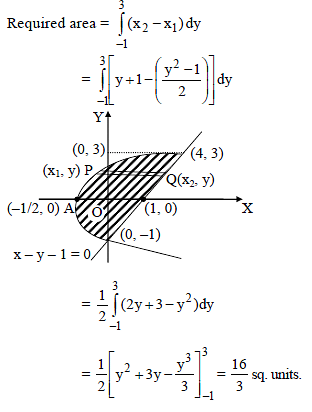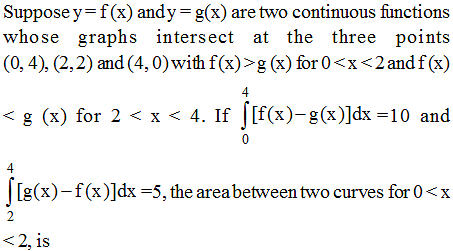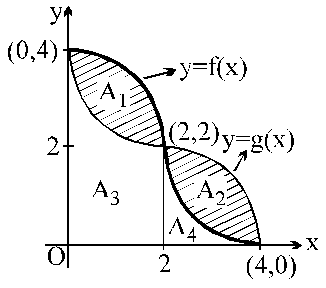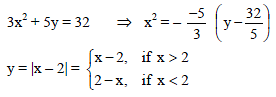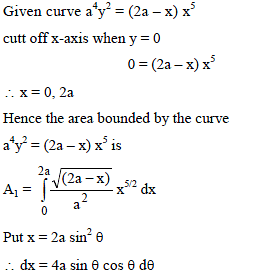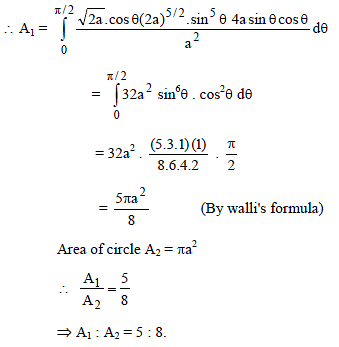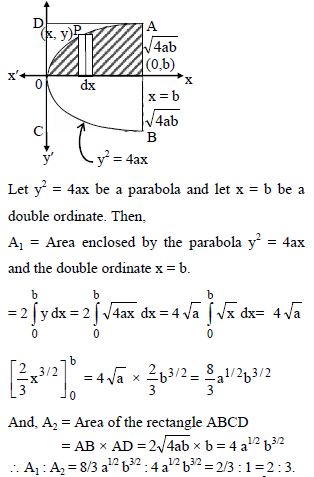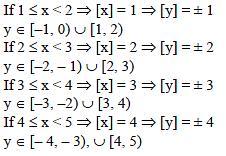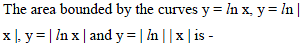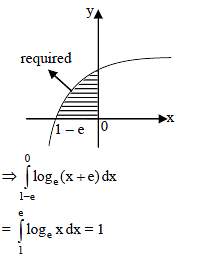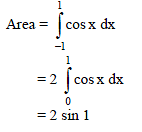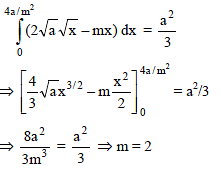Application of Integrals - 1 - JEE MCQ

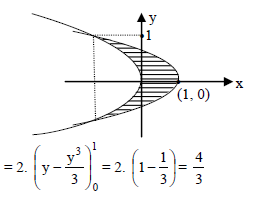
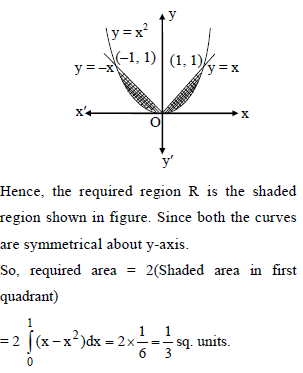
The area bounded by the parabola y = x² and the line y = x is

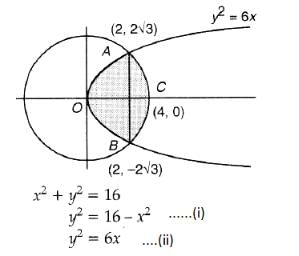
The area common to the circle x²+y² = 16 and the parabola y² = 6x is

The area of the region bounded by the curves y = |x−2|, x = 1 , x = 3 and the x – axis is

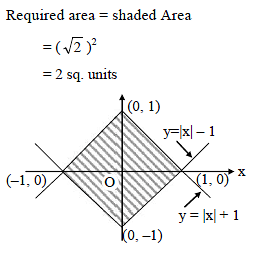
The area bounded by the curve y = | x | – 1 and y = – | x | + 1 is -

The area bounded by the curve y = x|x|, x-axis and the ordinates x = 1, x = –1 is given by

The ratio of the areas of two curves y = cos x and

y = cos 2x between x-axis from x = 0 to x = π/3 is

The area enclosed between the curves y = sin² x and y = cos²x in the interval 0 ≤ x ≤ π is -

The area of the plane region bounded by the curves x + 2y² = 0 and x + 3y² = 1 is equal to- 

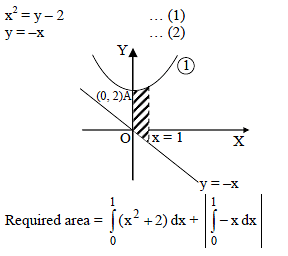
Area of the region bounded by the curves y = x² + 2, y = – x, x = 0 and x = 1 is -

Find the area bounded by x = 1/2, x = 2, y = log_e x and y = 2^x -

The area bounded by the curves y² = 2x + 1 and x – y – 1 = 0 is -

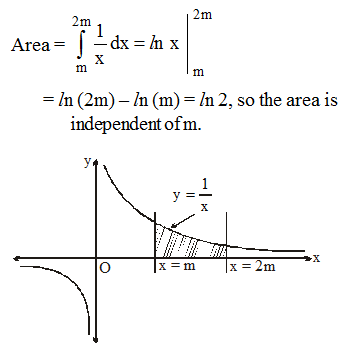
A region in the  xy  plane is bounded by the graph of  y = 1/x  , the x-axis, the line x = m, and the line x = 2m, m > 0. The area of this region

The area enclosed by the curves 3x² + 5y = 32 and y = | x – 2 | is -

The area of the region bounded by the curve a⁴y² = (2a – x) x⁵ is to that of the circle whose radius is a, is given by the ratio -

Ratio of the area cut off a parabola by any double ordinate is that of the corresponding rectangle contained by that double ordinate and its distance from the vertex is -

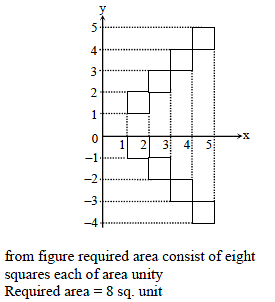
Area of region bounded by [x]² = [y]² if x ∈ [1, 5] where [.] represents the greatest integer function, is -

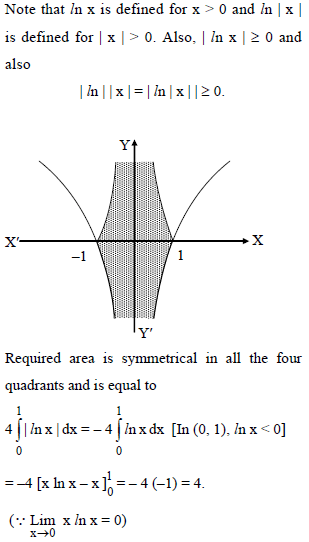
The area enclosed between the curve y = log_e(x + e) and the coordinate axes is-

The area of the bounded by y = cos x, y = 0, | x | = 1 is given by -

The value of m for which the area included between the curves y² = 4ax and y = mx equals a²/3 is