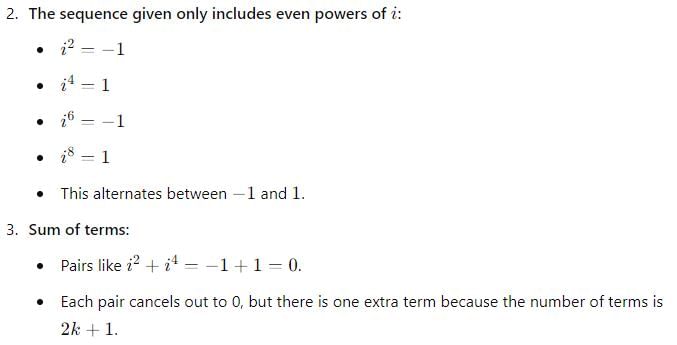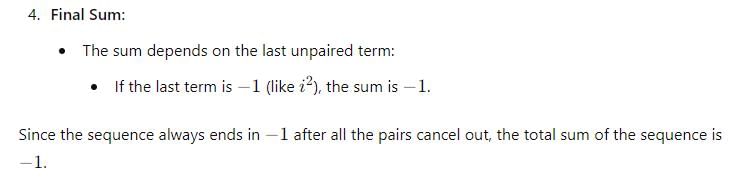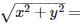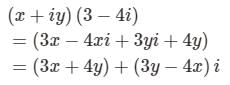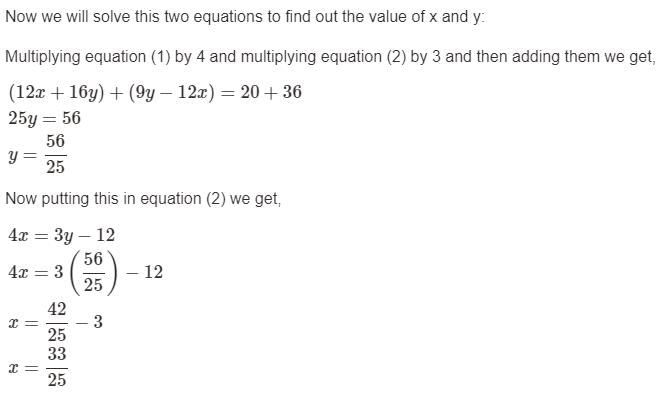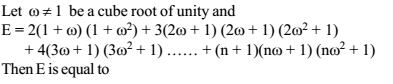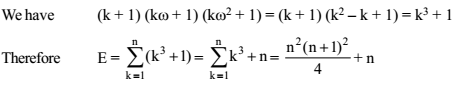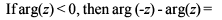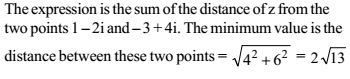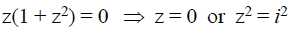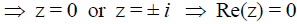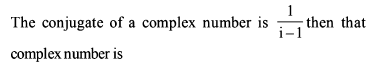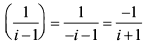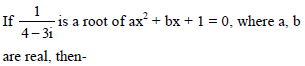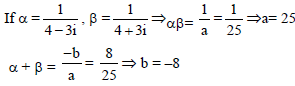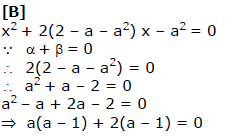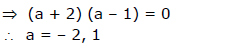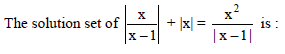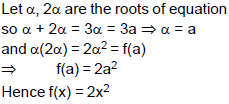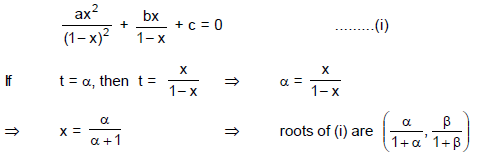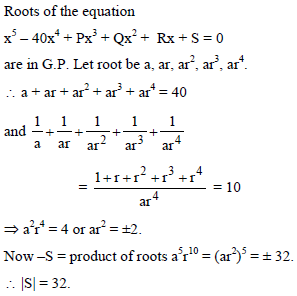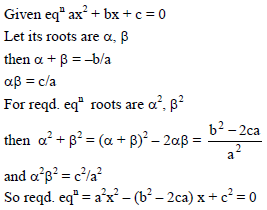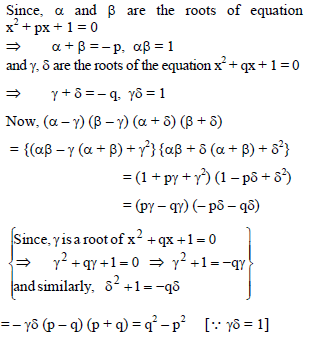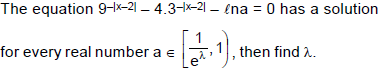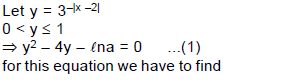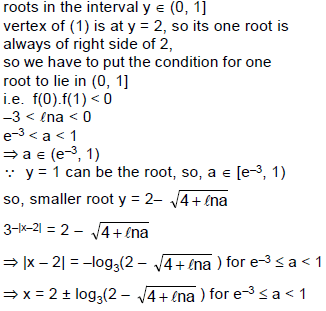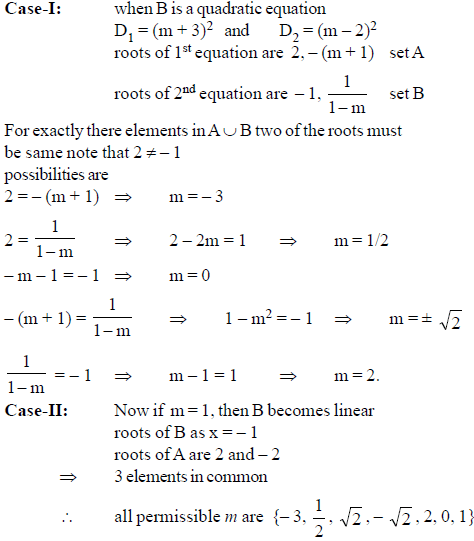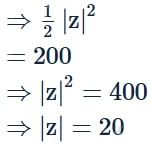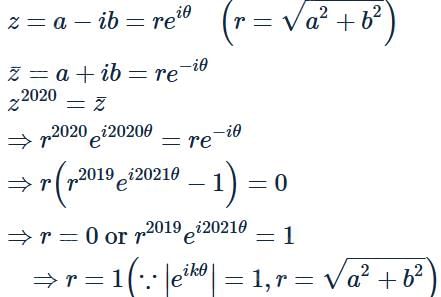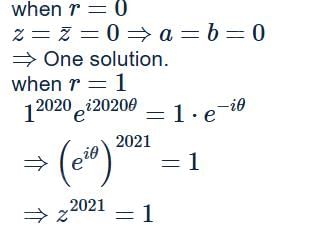Complex Numbers and Quadratic Equation - 1 - JEE MCQ

If (x + iy) (3 - 4i) = (5 + 12i), then 

The minimum value of | z – 1 + 2i | + | 4i – 3 – z | is

If z + z³ = 0 then which of the following must be true on the complex plane?

For what value of a the sum of roots of the eqn. x²+ 2 (2 – a – a²)x – a² = 0 is zero-

If the equations x² + px + q = 0 (p , q ∈ R) and x³ + 3x² + 5x + 3 = 0 have two roots common, then find the value of (p + q).

If for all real values of 'a' one root of the equation x² – 3ax + f(a) = 0 is double of the other, then f(x) is equal to

If α, β are the roots of the equation ax² + bx + c = 0, then the equation ax² – bx (x – 1) + c (x – 1)2 = 0 has roots

If the roots of x⁵ – 40x⁴ + Px³ + Qx² + Rx + S = 0 are in G.P. and sum of their reciprocals is 10, then |S| is -

The equation whose roots are the squares of the roots of the equation ax² + bx + c = 0 is

If α, β are the roots of x2 + px + 1 = 0 and γ, δ are the roots of x² + qx + 1 = 0, then q² – p² is equal to -

Let A = { x | x² + (m – 1)x – 2(m + 1) = 0, x ∈ R}

B = { x | (m – 1)x² + mx + 1 = 0, x ∈ R}

Find the number of values of m such that A ∪ B has exactly 3 distinct elements.

If the area of the triangle on the complex plane formed by the points z, iz and z + iz is 200 square units, then |z| is

If k + |k + z²| = |z|² where k is real, then a possible argument of z is

Number of ordered pairs (a,b) of real numbers such that (a+ib)²⁰²⁰ = a−ib
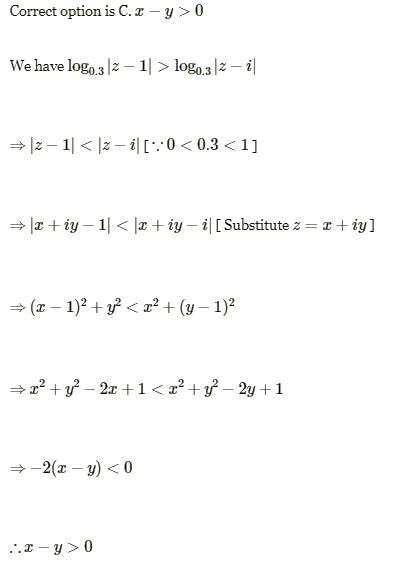