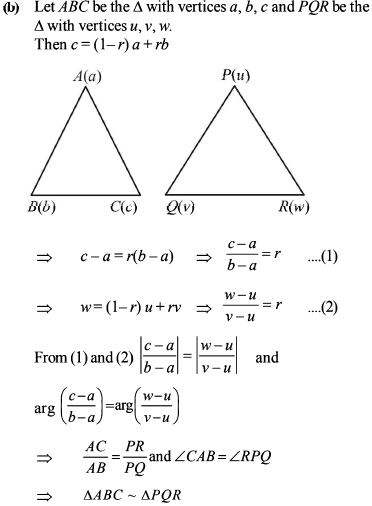
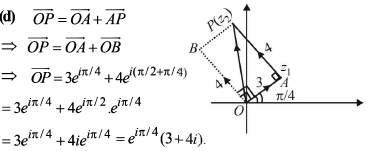
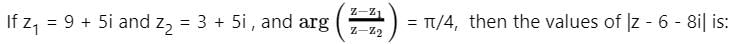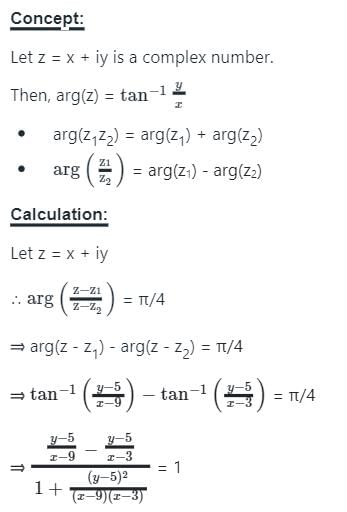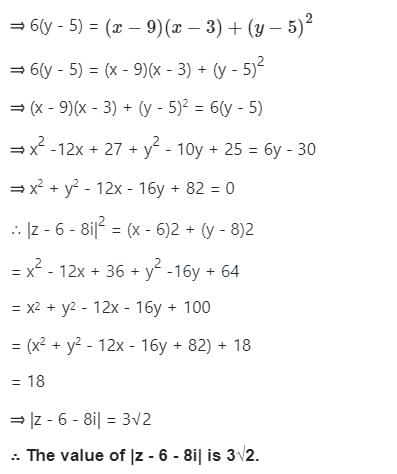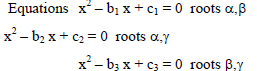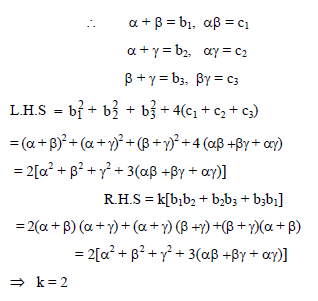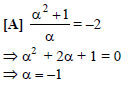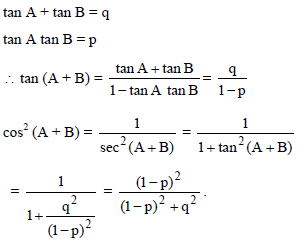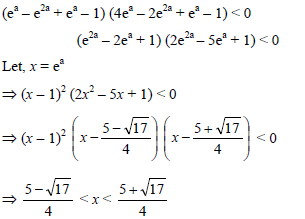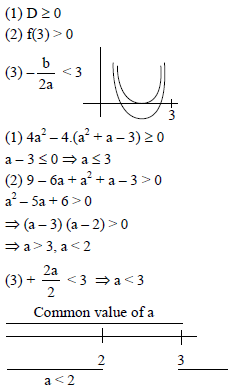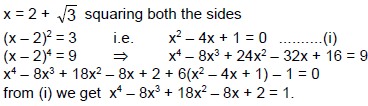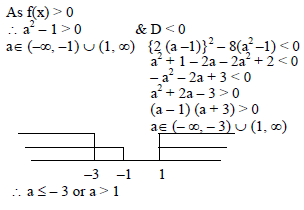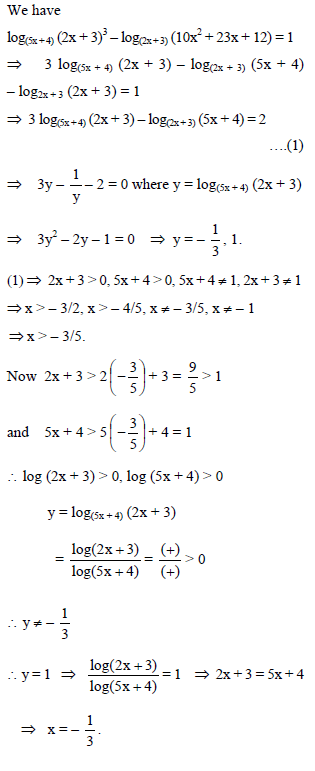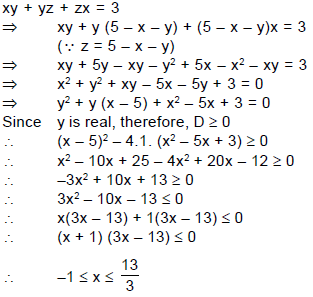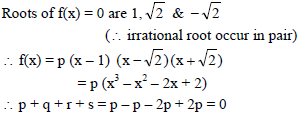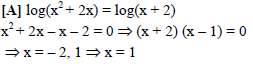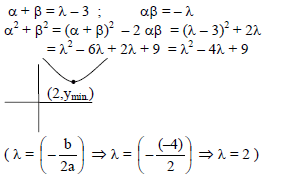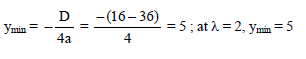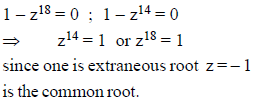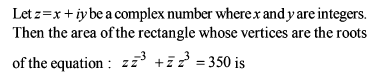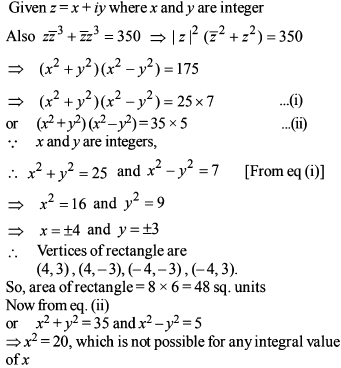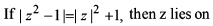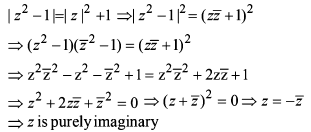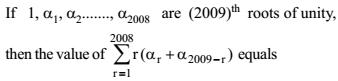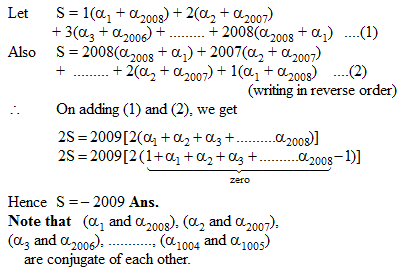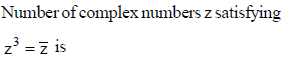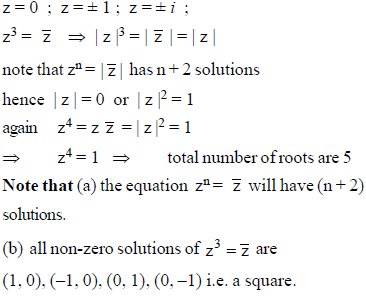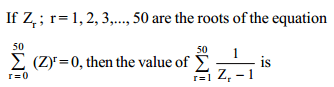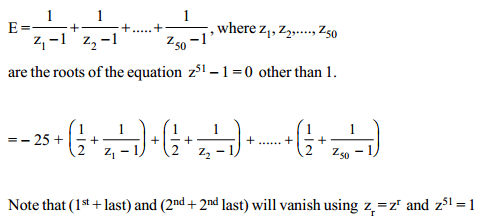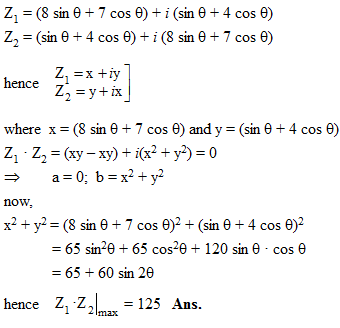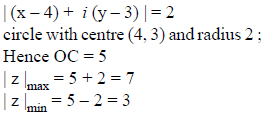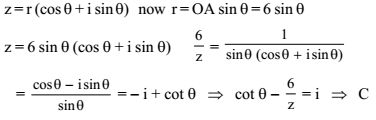Complex Numbers and Quadratic Equation - 2 - JEE MCQ
30 Questions MCQ Test - Complex Numbers and Quadratic Equation - 2
Each pair of equations from x2 – brx + cr = 0, r = 1, 2, 3 have a common root and the relation is given ∑b12 + 4 ∑c1 = k∑b1b2 then value of k is -
If the product of the roots of the equation αx2 + bx + α2 + 1 = 0 is –2, then equals -
If tan A and tan B are the roots of the quadratic x2 – qx + p = 0 then the value of cos2 (A + B) is -
The values of ‘a’ for which exactly one root of the equation eax2 – e2a x + ea – 1 = 0 lies between 1 and 2 are given by -
If roots of equation x2 – 2ax + (a2 + a – 3) = 0 are real and less than 3 then
The value of the expression x4 – 8x3 + 18x2 – 8x + 2 when x = 2 + √3 is
The values of 'a' for which (a2 – 1)x2 + 2 (a – 1) x + 2 is positive for any x is -
The set of real roots of the equation log(5x + 4) (2x + 3)3 – log(2x + 3) (10x2 + 23x + 12) = 1 is -
If x + y + z = 5 and xy + yz + zx = 3, then least and largest value of x are
The expression y = ax2 + bx + c has always the same sign as c if -
If p, q, r, s are rational numbers & roots of f(x) = 0 are eccentricities of a parabola & a rectangular hyperbola where f(x) = px3 + qx2 + rx + s, then p + q + r + s =
If r and s are positive, then roots of the equation x2 – rx – s =0 are -
Let α,β be the roots of x2 + (3 – λ)x – λ = 0. The value of λ for which α2 + β2 is minimum, is -
Number of values of z (real or complex) simultaneously satisfying the system of equations 1 + z + z2 + z3 + .......... + z17 = 0 and 1 + z + z2 + z3 + .......... + z13 = 0 is
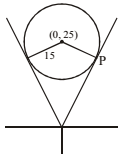
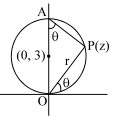
The complex number z having least positive argument which satisfy the condition |z – 25i | ≤ 15 is -
Let Z1 = (8 + i)sin θ + (7 + 4i)cos θ and Z2 = (1 + 8i)sin θ + (4 + 7i)cos θ are two complex numbers. If Z1 · Z2 = a + ib where a, b ∈ R then the largest value of (a + b) ∀ θ ∈ R, is
A point 'z' moves on the curve |z – 4 – 3 i| = 2 in an argand plane. The maximum and minimum values of |z| are