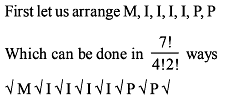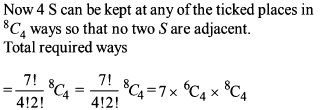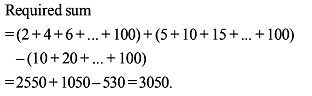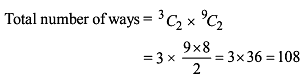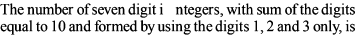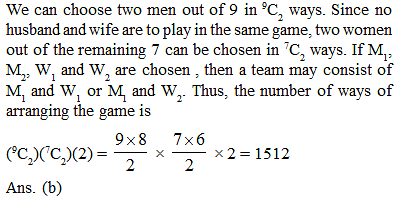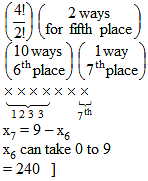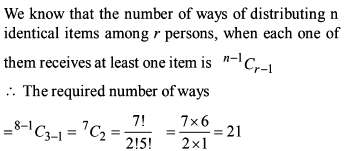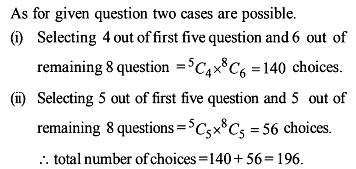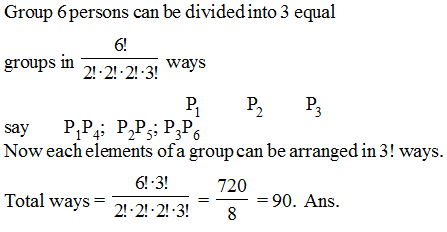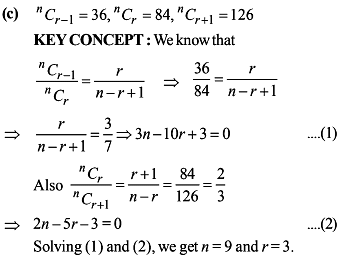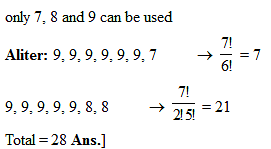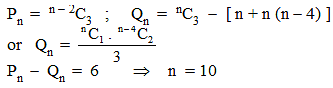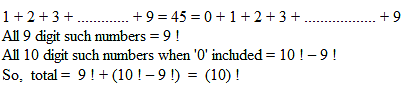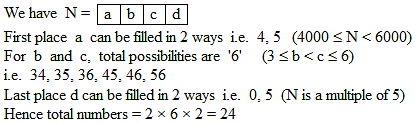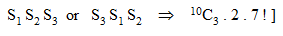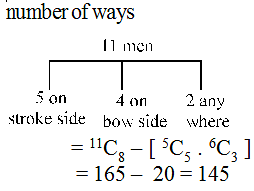Permutations and Combinations - 2 - JEE MCQ
30 Questions MCQ Test - Permutations and Combinations - 2
There are n white and n black balls marked 1, 2,......., n. The number of ways in which we can arrange these balls in a row so that neighbouring balls are of different colours is
f : {1, 2, 3, 4, 5} → {x, y, z, t}. Total number of on to functions ‘f’, is equal to -
The number of ways in which a mixed double game can be arranged from amongst 9 married couples if no husband and wife play in the same game is -
An old man while dialing a 7 digit telephone number remembers that the first four digits consists of one 1's, one 2's and two 3's. He also remembers that the fifth digit is either a 4 or 5 while has no memorising of the sixth digit, he remembers that the seventh digit is 9 minus the sixth digit. Maximum number of distinct trials he has to try to make sure that he dials the correct telephone number, is
In a jeep there are 3 seats in front and 3 in the back. Number of different ways can six persons of different heights be seated in the jeep, so that every one in front is shorter than the person directly behind is
Number of 7 digit numbers the sum of whose digits is 61 is
A four digit number is called a doublet if any of its digit is the same as only one neighbour. For example, 1221 is a doublet but 1222 is not. Find the number of such doublets.
Let Pn denotes the number of ways of selecting 3 people out of ' n ' sitting in a row , if no two of them are consecutive and Qn is the corresponding figure when they are in a circle . If Pn - Qn = 6 , then ' n ' is equal to :
Number of positive integers which have no two digits having the same value with sum of their digits being 45, is
Number of 4 digit numbers of the form N = abcd which satisfy following three conditions
(i) 4000 ≤ N < 6000
(ii) N is a multiple of 5
(iii) 3 ≤ b < c ≤ 6 is equal to
The number of positive integral solutions of the equation x1 x2 x3 x4 x5 = 1050, is
In a conference 10 speakers are present. If S1 wants to speak before S2 & S2 wants to speak after S3, then the number of ways all the 10 speakers can give their speeches with the above restriction if the remaining seven speakers have no objection to speak at any number is
Find the number of 4 digit numbers starting with 1 and having exactly two identical digits.
A crew of an eight oar boat has to be chosen out of 11 men five of whom can row on stroke side only, four on the bow side only, and the remaining two on either side. Find the different selections that can be made.